题目内容
用数学归纳法证明“ 能被3整除”的第二步中,
能被3整除”的第二步中, 时,为了使用归纳假设,应将
时,为了使用归纳假设,应将 变形为 从而可以用归纳假设去证明。
变形为 从而可以用归纳假设去证明。
 能被3整除”的第二步中,
能被3整除”的第二步中, 时,为了使用归纳假设,应将
时,为了使用归纳假设,应将 变形为 从而可以用归纳假设去证明。
变形为 从而可以用归纳假设去证明。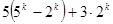 或
或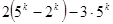
假设n=k时命题成立.
即:
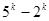 被3整除.
被3整除.当n=k+1时,
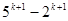 =
=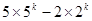
=
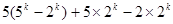
=
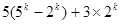
或
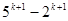 =
=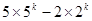
=
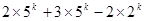
=

故答案为:
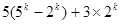 或
或

练习册系列答案
相关题目
题目内容
 能被3整除”的第二步中,
能被3整除”的第二步中, 时,为了使用归纳假设,应将
时,为了使用归纳假设,应将 变形为 从而可以用归纳假设去证明。
变形为 从而可以用归纳假设去证明。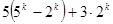 或
或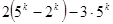
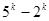 被3整除.
被3整除.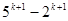 =
=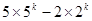
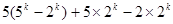
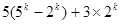
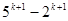 =
=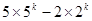
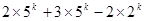

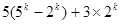 或
或
