题目内容
甲、乙等五名大运会志愿者被随机分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列及数学期望.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列及数学期望.
(1)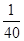 (2)
(2)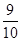 (3)
(3)
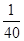 (2)
(2)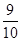 (3)
(3)
(1)记“甲、乙两人同时参加A岗位服务”为事件A1,
则P(A1)=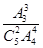 =
=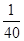 .
.
故甲、乙两人同时参加A岗位服务的概率为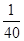 .
.
(2)记“甲、乙两人在同一岗位服务”为事件A2,
则P(A2)=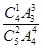 =
=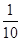 .
.
故甲、乙两人不在同一岗位服务的概率为P(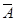 2)=1-P(A2)=
2)=1-P(A2)=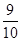 .
.
(3)由题知,随机变量ξ的所有可能取值为1,2,则P(ξ=2)=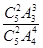 =
=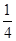 ,P(ξ=1)=1-P(ξ=2)=
,P(ξ=1)=1-P(ξ=2)=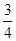 .故ξ的分布列为
.故ξ的分布列为
数学期望Eξ=1×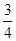 +2×
+2×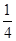 =
=
则P(A1)=
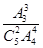 =
=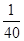 .
.故甲、乙两人同时参加A岗位服务的概率为
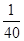 .
.(2)记“甲、乙两人在同一岗位服务”为事件A2,
则P(A2)=
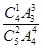 =
=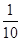 .
.故甲、乙两人不在同一岗位服务的概率为P(
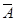 2)=1-P(A2)=
2)=1-P(A2)=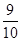 .
.(3)由题知,随机变量ξ的所有可能取值为1,2,则P(ξ=2)=
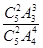 =
=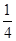 ,P(ξ=1)=1-P(ξ=2)=
,P(ξ=1)=1-P(ξ=2)=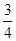 .故ξ的分布列为
.故ξ的分布列为| ξ | 1 | 2 |
| P | 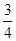 | 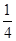 |
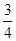 +2×
+2×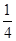 =
=

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 其中
其中

 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利 的可能性为
的可能性为 ,亏损
,亏损 的可能性为
的可能性为 ;位于二类风区的B项目获利
;位于二类风区的B项目获利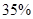 的可能性为
的可能性为 的可能性是
的可能性是 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
. 和
和 ,试写出随机变量
,试写出随机变量 ,
, ;
; 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投 的最大值.
的最大值. 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 .
. ,则D(ξ)的值是( )
,则D(ξ)的值是( ) (C)
(C) (D)
(D)
 ;如果出现一奇一偶,则将它们的差的绝对值记为
;如果出现一奇一偶,则将它们的差的绝对值记为 ,且P(A)=p令随机变量X=
,且P(A)=p令随机变量X= ,则X的方差V(X)等于________.
,则X的方差V(X)等于________.