��Ŀ����
��20����f(x)�Ƕ�����[0, 1]�ϵĺ�����������x*��(0��1)��ʹ��f(x)��[0, x*]�ϵ�����������[x*��1]�ϵ����ݼ������f(x)Ϊ[0, 1]�ϵĵ��庯����x*Ϊ��㣬������������Ϊ�������䣮�������[0��1]�ϵĵ��庯��f(x)�������о������京�����䳤�ȵķ�����
��I��֤�����������x1��x2��(0��1)��x1��x2����f(x1)��f(x2)����(0��x2)Ϊ�������䣻��f(x1)��f(x2)����(x1��1)Ϊ�������䣻
��II���Ը�����r��0��r��0.5����֤��������x1��x2��(0��1)������x2��x1��2r��ʹ���ɣ�I����ȷ���ĺ�������ij��Ȳ����� 0.5��r��
��III��ѡȡx1��x2��(0, 1)��x1��x2���ɣ�I����ȷ����������Ϊ(0��x2)��(x1��1)�������õĺ���������ѡȡx3����x3��x1��x3��x2���Ƶؿ�ȷ��һ���µĺ������䣮�ڵ�һ��ȷ���ĺ�������Ϊ(0��x2)������£���ȷ��x1��x2��x3��ֵ����������֮��ľ���ֵ��С��0.02����ʹ���µĺ�������ij������̵�0.34.
�����䳤�ȵ���������Ҷ˵�����˵�֮�
��20����I��֤������x*Ϊf(x) �ķ�㣬���ɵ��庯�������֪��f(x)��[0, x*]�ϵ�����������[x*, 1]�ϵ����ݼ���
��f(x1)��f(x2)ʱ������x*![]() (0, x2)����x1<x2��x*���Ӷ�f(x*)��f(x2)>f(x1)��
(0, x2)����x1<x2��x*���Ӷ�f(x*)��f(x2)>f(x1)��
����f(x1)��f(x2)ì�ܣ�����x*��(0, x2)����(0, x2)�Ǻ�������.
��f(x1)��f(x2)ʱ������x*![]() ( x1, 1)����x*��x1<x2���Ӷ�f(x*)��f(x1)>f(x2)��
( x1, 1)����x*��x1<x2���Ӷ�f(x*)��f(x1)>f(x2)��
����f(x1)��f(x2)ì�ܣ�����x*��(x1, 1)����(x1, 1)�Ǻ�������.
��II��֤�����ɣ�I���Ľ��ۿ�֪��
��f(x1)��f(x2)ʱ����������ij���Ϊl1��x2��
��f(x1)��f(x2)ʱ����������ij���Ϊl2=1��x1��
������������������������
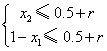 ��
��
�ɢٵ� 1��x2��x1��1+2r����x2��x1��2r.
����Ϊx2��x1��2r������
x2��x1=2r, ��
���ڴ���ٵ�
x1��0.5��r, x2��0.5��r�� ��
�ɢٺ͢۽�� x1��0.5��r�� x2��0.5��r��
������ʱ��������ij���l1��l2��0.5��r��������x1��x2ʹ����ȷ���ĺ�������ij��Ȳ�����0.5��r��
��III���⣺����ѡ���x1��x2��x1<x2���ɣ�II����֪
x1��x2��1�� ��
�ڵ�һ��ȷ���ĺ�������Ϊ(0, x2)������£�x3��ȡֵӦ����
x3��x1��x2�� ��
�ɢ���ݿɵ�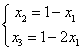 ,
,
��x1>x3ʱ����������ij���Ϊx1��
������x1��x3��0.02����x1��(1��2x1)��0.02���Ӷ�x1��0.34��
��ˣ�Ϊ�˽���������ij������̵�0.34��ֻ��ȡx1��0.34��x2��0.66��x3=0.32��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�