题目内容
已知O是坐标原点，点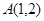
，若点
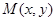为平面区域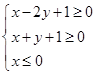
上的一个动点 ，则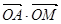
的最大值是（ ▲ ）
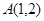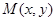，若点为平面区域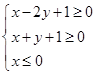上的一个动点 ，则
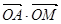的最大值是（ ▲ ）| A．-1 | B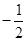． | C．0 | D．1 |
D
析：首先画出可行域，z= 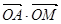代入坐标变为z=x+2y，即y=
x+
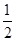z，
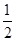z表示斜率为-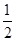的直线在y轴上的截距，故求z的最大值，即平移直线y=-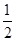x与可行域有公共点时直线在y轴上的截距的最大值即可．
解答：解：如图所示：
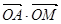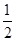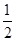z==x+2y，即y=-x+z，
首先做出直线l0：y=-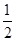x，将l0平行移动，当经过A（0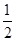，）点时在y轴上的截距最大，从而z最大．
因为B（0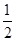，），故z的最大值为z=0+2×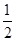=1．
故选D．
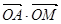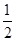代入坐标变为z=x+2y，即y=x+z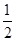， z表示斜率为-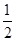的直线在y轴上的截距，故求z的最大值，即平移直线y=-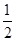x与可行域有公共点时直线在y轴上的截距的最大值即可．解答：解：如图所示：
z=
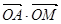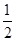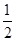=x+2y，即y=-x+z，首先做出直线l0：y=-
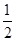x，将l0平行移动，当经过A（0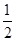，）点时在y轴上的截距最大，从而z最大．因为B（0，
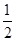），故z的最大值为z=0+2×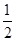=1．故选D．
练习册系列答案
相关题目
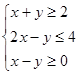，所围成的平面区域的面积为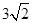
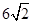
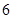
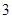
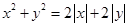所围成的面积是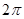
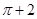
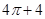
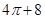
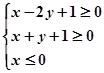，则x+2y的最大值是（ ）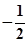
、
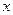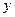满足约束条件：
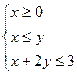则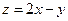
的最优解为( )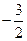
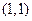
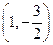
，则t＝x－y的取值范围是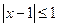
表示的平面区域与抛物线
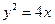组成的封闭区域的面积是 
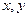满足条件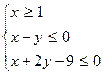
，若目标函数
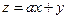仅在点（3，3）
的取值范围
是___________________.