题目内容
下列几种说法正确的是
①函数y=cos(
-3x)的递增区间是[-
+
,
+
],k∈Z;
②函数f(x)=5sin(2x+?),若f(a)=5,则f(a+
)<f(a+
);
③函数f(x)=3tan(2x-
)的图象关于点(
,0)对称;
④将函数y=sin(2x+
)的图象向右平移
个单位,得到函数y=sin2x的图象;
⑤在同一平面直角坐标系中,函数y=sin(
+
)(x∈[0,2π])的图象和直线y=
的交点个数是1个.
①③⑤
①③⑤
(将你认为正确的序号全部填在横线上)①函数y=cos(
| π |
| 4 |
| π |
| 4 |
| 2kπ |
| 3 |
| π |
| 12 |
| 2kπ |
| 3 |
②函数f(x)=5sin(2x+?),若f(a)=5,则f(a+
| π |
| 12 |
| 5π |
| 6 |
③函数f(x)=3tan(2x-
| π |
| 3 |
| 5π |
| 12 |
④将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
⑤在同一平面直角坐标系中,函数y=sin(
| x |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
分析:对于①,函数的解析式即y=cos(3x-
),由 2kπ-π≤3x-
≤2kπ,k∈z,求得它的增区间,比较可得①正确.
对于②,由于x=a 是函数的对称轴,且函数的周期等于π,可得 f(a+
)>f(a+
),故②不正确.
对于③,由于点(
,0)在函数图象上,结合图象可得函数图象关于点(
,0)对称,故③正确.
对于④将函数y=sin(2x+
)的图象向右平移
个单位,得到函数y=sin(2x-
) 的图象,故④不正确.
对于⑤由y=sin(
+
)=-cos
,画出y=-cos
,x∈[0,2π]的图象,显然图象和y=
只有1个交点,
故⑤正确.
| π |
| 4 |
| π |
| 4 |
对于②,由于x=a 是函数的对称轴,且函数的周期等于π,可得 f(a+
| π |
| 12 |
| 5π |
| 6 |
对于③,由于点(
| 5π |
| 12 |
| 5π |
| 12 |
对于④将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
对于⑤由y=sin(
| x |
| 2 |
| 3π |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
故⑤正确.
解答:解:对于①函数y=cos(
-3x)=cos(3x-
),由 2kπ-π≤3x-
≤2kπ,k∈z,
解得 -
+
≤x ≤
+
,k∈z.
故函数的递增区间是 [-
+
,
+
] ,k∈Z,故①正确.
对于②函数f(x)=5sin(2x+?),若f(a)=5,故x=a 是函数的对称轴,且函数的周期等于π,
故函数在[a-
,a+
]上是单调增函数.
∵f(a+
)=f(a-
),f(a+
) =f(a-
),a-
<a-
,
∴f( a-
)<f( a-
),即 f(a+
)>f(a+
),故②不正确.
对于③函数f(x)=3tan(2x-
),由于点(
,0)在图象上,结合图象可得函数图象关于点(
,0)对称,
故③正确.
对于④将函数y=sin(2x+
)的图象向右平移
个单位,得到函数y=sin[2(x-
)+
]=sin(2x-
) 的图象,
故④不正确.
对于⑤∵y=sin(
+
)=-cos
,x∈[0,2π],画出y=-cos
,x∈[0,2π]的图象,显然图象和y=
只有1个交点,故⑤正确.
故答案为:①③⑤.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解得 -
| π |
| 4 |
| 2kπ |
| 3 |
| π |
| 12 |
| 2kπ |
| 3 |
故函数的递增区间是 [-
| π |
| 4 |
| 2kπ |
| 3 |
| π |
| 12 |
| 2kπ |
| 3 |
对于②函数f(x)=5sin(2x+?),若f(a)=5,故x=a 是函数的对称轴,且函数的周期等于π,
故函数在[a-
| π |
| 2 |
| π |
| 2 |
∵f(a+
| π |
| 12 |
| π |
| 12 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
∴f( a-
| π |
| 6 |
| π |
| 12 |
| π |
| 12 |
| 5π |
| 6 |
对于③函数f(x)=3tan(2x-
| π |
| 3 |
| 5π |
| 12 |
| 5π |
| 12 |
故③正确.
对于④将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故④不正确.
对于⑤∵y=sin(
| x |
| 2 |
| 3π |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
只有1个交点,故⑤正确.
故答案为:①③⑤.
点评:本题主要考查三角函数的对称性和单调性,以及函数图象的变换,三角函数的内容比较琐碎,要记忆的比较多,平时要注意公式的记忆和基础知识的积累,掌握基本知识是解好这类题目的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在正方体ABCD-A1B1C1D1中,下列几种说法正确的是( )
| A、A1C1⊥AD | B、D1C1⊥AB | C、AC1与DC成45°角 | D、A1C1与B1C成60°角 |
 的递增区间是
的递增区间是 ;
; ;
;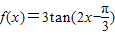 的图象关于点
的图象关于点 对称;
对称; 的图象向右平移
的图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象; 的图象和直线
的图象和直线 的交点个数是1个.
的交点个数是1个.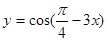 的递增区间是
的递增区间是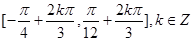 ;Zxxk
;Zxxk ,若
,若 ,则
,则 ;
; 的图象关于点
的图象关于点 对称;
对称; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴; 的图象可由函数
的图象可由函数 的图象向右平移
的图象向右平移 个单位得到;
个单位得到;