题目内容
已知命题p：“存在a∈R，使函数f(x)＝ax2－4x(a＞0)在(－∞，2]上单调递减”，命题q：“存在a∈R，使
x∈R,16x2－16(a－1)x＋1≠0”.若命题“p∧q”为真命题，求实数a的取值范围.
p为真：当a＞0时，只需对称轴x＝－
＝
在区间(－∞，2]的右侧，即≥2，
∴0＜a≤1，
q为真：命题等价于：方程16x2－16(a－1)x＋1＝0无实根.
Δ＝[16(a－1)]2－4×16＜0，∴
＜a＜
，
∵命题“p∧q”为真命题，∴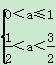
，∴＜a≤1.
练习册系列答案
相关题目