Question

已知y=log_a(2－ax)在区间{0，1}上是x的减函数，求a的取值范围．

 

Answer 1

【答案】

1＜a＜2

【解析】主要考查对数函数的概念、图象和性质。

解：先求函数定义域：由2－ax＞0，得ax＜2

又a是对数的底数，

∴a＞0且a≠1，∴x＜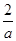

由递减区间[0，1]应在定义域内可得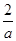＞1，∴a＜2

又2－ax在x∈[0，1]是减函数

∴y=log_a(2－ax)在区间[0，1]也是减函数，由复合函数单调性可知：a＞1

∴1＜a＜2