题目内容
解不等式: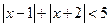
解:分别求 的零点,即
的零点,即
由 把数轴分成三部分:
把数轴分成三部分:
当 时,原不等式即
时,原不等式即
解得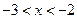
当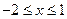 时,原不等式即
时,原不等式即
因为 恒成立,所以
恒成立,所以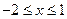 时原不等式成立;
时原不等式成立;
当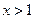 时,原不等式即
时,原不等式即 ,
,
解得
综上,原不等式的解集是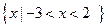
解析

练习册系列答案
相关题目
已知x,y均为正数且x+2y=xy,则( ).
A.xy+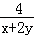 有最小值4 有最小值4 | B.xy+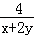 有最小值3 有最小值3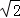 |
C.x+2y+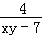 有最小值11 有最小值11 | D.xy﹣7+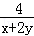 有最小值11 有最小值11 |
设 ,且
,且 ,若
,若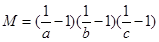 ,则必有
,则必有
A. | B. | C. | D. |
已知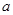 、
、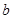 都是正实数,函数
都是正实数,函数 的图象过
的图象过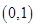 点,则
点,则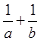 的最小值是( )
的最小值是( )
A.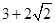 | B.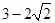 | C.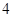 | D. |

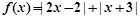 .
.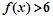 ;
;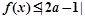 的解集不是空集,试求
的解集不是空集,试求 的取值范围.
的取值范围. 的不等式:
的不等式: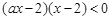
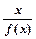 ≤1的解集
≤1的解集 。
。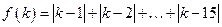 ,
,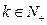 且
且