题目内容
给出下列命题:
①若f(x)=2x3+3的反函数为f-1(x),则f-1(5)=1;
②过原点作圆x2+y2-12x+9=0的两切线,则两切线所夹的劣弧长为2
π;
③在△ABC中,已知a=5,b=6,A=30°,则B有一解且B=arcsin
;
④在样本频率分布直方图中,共有三个长方形,其面积由小到大构成等差数列{an},且a2+a3=0.8,则最大的长方形的面积为
其中正确命题的序号为
①若f(x)=2x3+3的反函数为f-1(x),则f-1(5)=1;
②过原点作圆x2+y2-12x+9=0的两切线,则两切线所夹的劣弧长为2
| 3 |
③在△ABC中,已知a=5,b=6,A=30°,则B有一解且B=arcsin
| 3 |
| 5 |
④在样本频率分布直方图中,共有三个长方形,其面积由小到大构成等差数列{an},且a2+a3=0.8,则最大的长方形的面积为
| 7 |
| 15 |
其中正确命题的序号为
①④
①④
.分析:根据原函数与反函数之间的关系得到①正确,根据弧长的运算得到②不正确,根据三角形解的个数的判断得到③不正确,根据频率分布直方图得到④正确.
解答:解:若f(x)=2x3+3的反函数为f-1(x),则f-1(5)=1;把1代入原函数得到函数值时5,故①正确,
过原点作圆x2+y2-12x+9=0的两切线,
过圆心做切线的垂线,根据组成的直角三角形三边之间的关系,得到两条切线所夹的角是60°,
根据原定周长乘以
,弧长是
×2×π×3
=
π,故②不正确,
则两切线所夹的劣弧长为2
π;
在△ABC中,已知a=5,b=6,A=30°,
∵6>5>6×sin30°
则B有两解,故③不正确,
在样本频率分布直方图中,共有三个长方形,其面积由小到大构成等差数列{an},
且a2+a3=0.8,a1=0.2,d=
,则最大的长方形的面积为0.2+
=
,故④正确,
综上可知①④正确,
故答案为:①④
过原点作圆x2+y2-12x+9=0的两切线,
过圆心做切线的垂线,根据组成的直角三角形三边之间的关系,得到两条切线所夹的角是60°,
根据原定周长乘以
| 1 |
| 6 |
| 1 |
| 6 |
| 3 |
| 3 |
则两切线所夹的劣弧长为2
| 3 |
在△ABC中,已知a=5,b=6,A=30°,
∵6>5>6×sin30°
则B有两解,故③不正确,
在样本频率分布直方图中,共有三个长方形,其面积由小到大构成等差数列{an},
且a2+a3=0.8,a1=0.2,d=
| 4 |
| 30 |
| 8 |
| 30 |
| 7 |
| 15 |
综上可知①④正确,
故答案为:①④
点评:本题考查的知识点比较多,特别注意对于解三角形的考查和对于弧长的考查,本题解题的关键是对于所给的四个命题逐一的判断,本题是一个中档题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
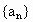 成等比数列,
成等比数列,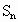 是前n项和,则
是前n项和,则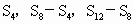 成等比数列;
成等比数列;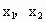 ,若
,若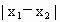 的最小值为π,则ω的值为2,θ的值为
的最小值为π,则ω的值为2,θ的值为 ;
;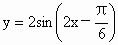 的图象的一个对称点是
的图象的一个对称点是 .
.