题目内容
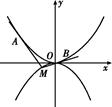
己知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且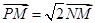 .
.
(1)求点N的轨迹C的方程;
(2)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则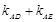 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
(1) 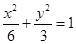 (2)
(2) 
解析试题分析:(1) 求动点轨迹方程的步骤,一是设所求动点坐标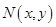 ,涉及两个动点问题,往往是通过相关点法求对应轨迹方程,此时也要设已知轨迹上的动点
,涉及两个动点问题,往往是通过相关点法求对应轨迹方程,此时也要设已知轨迹上的动点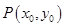 ,则
,则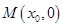 ,二是列出动点满足的条件
,二是列出动点满足的条件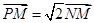 ,用未知动点坐标表示已知动点坐标,即
,用未知动点坐标表示已知动点坐标,即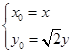 ,三是代入化简,
,三是代入化简,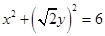 ,四是去杂,主要看是否等价转化,本题无限制条件, (2)定值问题,往往是坐标化简问题,即多参数消元问题. 利用斜率公式,直线方程化简
,四是去杂,主要看是否等价转化,本题无限制条件, (2)定值问题,往往是坐标化简问题,即多参数消元问题. 利用斜率公式,直线方程化简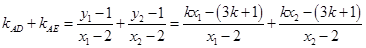
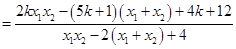 ,再利用韦达定理
,再利用韦达定理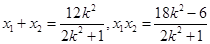 代入化简得常数
代入化简得常数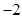 ,从过程看是四元变为二元,再变为一元,最后变为常数,一个逐步消元的运算过程,有运算量,无思维量.
,从过程看是四元变为二元,再变为一元,最后变为常数,一个逐步消元的运算过程,有运算量,无思维量.
试题解析:(1)设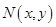 ,
,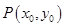 ,则
,则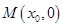 ,
,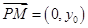 ,
,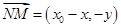
由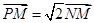 ,得
,得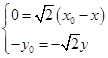 ,
,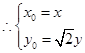 3分
3分
由于点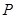 在圆
在圆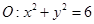 上,则有
上,则有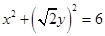 ,即
,即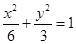 .
.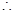 点
点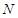 的轨迹
的轨迹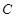 的方程为
的方程为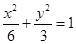 . 6分
. 6分
(2) 设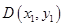 ,
,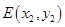 ,过点
,过点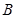 的直线
的直线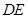 的方程为
的方程为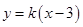 ,
,
由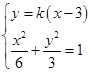 消去
消去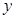 得:
得: 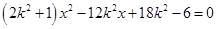 ,其中
,其中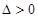
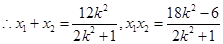 ; 8分
; 8分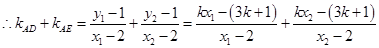
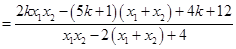 10分
10分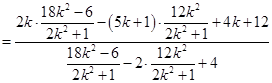
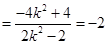
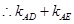 是定值
是定值 . 13分
. 13分
考点:动点轨迹,定值问题

练习册系列答案
相关题目
 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3. 时,切线MA的斜率为-
时,切线MA的斜率为- .
.
 +
+ =1(a>b>0)的左、右顶点分别为A,B,点P是双曲线C2:
=1(a>b>0)的左、右顶点分别为A,B,点P是双曲线C2: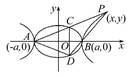
 +
+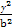 =1(a>b>0)的一个顶点A(2,0),离心率为
=1(a>b>0)的一个顶点A(2,0),离心率为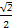 ,直线y=k(x-1)与椭圆C交于不同的两点M,N.
,直线y=k(x-1)与椭圆C交于不同的两点M,N.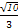 时,求k的值.
时,求k的值.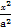 +
+ =1(a>b>0).
=1(a>b>0). ,求椭圆的标准方程.
,求椭圆的标准方程.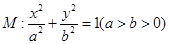 的离心率为
的离心率为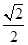 ,且经过点
,且经过点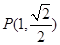 过坐标原点的直线
过坐标原点的直线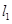 与
与 均不在坐标轴上,
均不在坐标轴上,
 =λ,求λ的取值范围.
=λ,求λ的取值范围.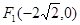 和
和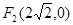 ,长轴长为6,设直线
,长轴长为6,设直线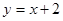 交椭圆C于A、B两点,求线段AB的中点坐标
交椭圆C于A、B两点,求线段AB的中点坐标