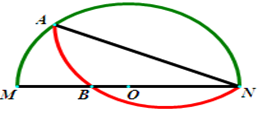
题目内容
平面 与球O相交于周长为
与球O相交于周长为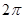 的⊙
的⊙ ,A、B为⊙
,A、B为⊙ 上两点,若∠AOB=
上两点,若∠AOB= ,且A、B的球面距离为
,且A、B的球面距离为 ,则
,则 的长度为( )
的长度为( )
A.1 B. C.
C. D.2
D.2
A
解析试题分析:令球的半径为R,则其过球心的截面(圆)的周长为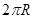 ,又因为A、B两点的球面距离为
,又因为A、B两点的球面距离为 ,且∠AOB=
,且∠AOB= ,所以可得
,所以可得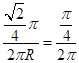 ,解得
,解得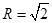 。又由题意得,⊙
。又由题意得,⊙ 的半径为
的半径为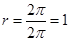 ,所以由勾股定理得,
,所以由勾股定理得, 的长度为
的长度为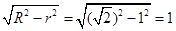 。
。
考点:球面距离。
点评:立体几何空间想象能力要求较高。

练习册系列答案
相关题目
圆内接平行四边形一定是
| A.正方形 | B.菱形 |
| C.等腰梯形 | D.矩形 |
如图所示,若圆内接四边形的对角线相交于E,则图中相似三角形有( ).
| A.1对 | B.2对 |
| C.3对 | D.4对 |
如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE等于( ).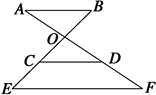
| A.9 | B.10 |
| C.11 | D.12 |
如图4,正方形ABCD中,E是AB上任一点,作EF⊥BD 于F,则
于F,则 EF︰BE=( )
EF︰BE=( )
A. | B. | C. | D. |
 折叠过来和直径MN交于点B,如
折叠过来和直径MN交于点B,如