题目内容
已知正项数列 的首项
的首项 ,前
,前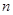 项和
项和 满足
满足 .
.
(Ⅰ)求证: 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ) ;(Ⅱ )
;(Ⅱ ) .
.
【解析】
试题分析:(Ⅰ)求证 为等差数列,只需证
为等差数列,只需证 等于常数,由
等于常数,由 ,而
,而 ,代入整理可得
,代入整理可得 为等差数列,从而求出数列
为等差数列,从而求出数列 的通项公式
的通项公式 ;(Ⅱ)不等式
;(Ⅱ)不等式 恒成立,转化为求
恒成立,转化为求 的最大值,而
的最大值,而 的前
的前 项和为
项和为 可用拆项相消法求得
可用拆项相消法求得 的最大值,从而解一元二次不等式得实数
的最大值,从而解一元二次不等式得实数 的取值范围.
的取值范围.
试题解析:(Ⅰ)证明:当 时,
时, ,又
,又 ,
,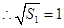 ,因为
,因为 ,
,
 ,
,
 , 即
, 即 ,
, ,所以数列
,所以数列 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
由此可得 ,由
,由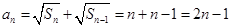 ,当
,当 时,
时, 也适合,所以
也适合,所以 ;
;
(Ⅱ)因为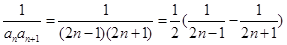 ,
,
所以, ,
, ,对任意的
,对任意的 ,不等式
,不等式 恒成立,
恒成立, ,解得
,解得 ,
,
所以对任意的 ,不等式
,不等式 恒成立,实数
恒成立,实数 的取值范围
的取值范围 .
.
考点:1、等差数列的证明,2、 与
与 的关系,3、求数列的通项公式,4、数列求和,5、解一元二次不等式.
的关系,3、求数列的通项公式,4、数列求和,5、解一元二次不等式.

练习册系列答案
相关题目
 的首项
的首项 ,前
,前 项和
项和 满足
满足
 .
. 的前
的前 ,求证:
,求证: .
. 的首项
的首项 前
前 项和为
项和为 ,且满足
,且满足 .
.
 取出三个数构成以正整数为公比的递增等比数列,放回后再取出三个数构成以正整数为公比的递增等比数列,相同的数列只取一次,按照上述取法取下去,直到取完所有满足条件的数列为止。求满足上述条件的所有的不同数列的和M.
取出三个数构成以正整数为公比的递增等比数列,放回后再取出三个数构成以正整数为公比的递增等比数列,相同的数列只取一次,按照上述取法取下去,直到取完所有满足条件的数列为止。求满足上述条件的所有的不同数列的和M.