题目内容
下列四个个命题，其中正确的命题是（ ）
分析：利用三角函数的性格性质进行判断．
解答：解：A．函数y=cotx在其定义域内不单调性，所以A错误．
B．函数y=sin（2x+
）的最小正周期是π，所以y=|sin（2x+
）|的最小正周期是
，所以B错误．
C．函数y=cosx在每个区间[2kπ+π，2kπ+
]（k∈z）上是增函数，所以C正确．
D．因为函数y=tan（x+
）是非奇非偶函数，所以D错误．
故选C．
B．函数y=sin（2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
C．函数y=cosx在每个区间[2kπ+π，2kπ+
| 7π |
| 4 |
D．因为函数y=tan（x+
| π |
| 4 |
故选C．
点评：本题主要考查三角函数的图象和性质的应用，要求熟练掌握相关的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
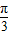)|的最小正周期是π
](k∈z)上是增函数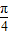
)是奇函数
）|的最小正周期是π
]（k∈z）上是增函数
）是奇函数