题目内容
已知函数f (x)=alnx+x2 (a为实常数).
(Ⅰ)若a=-2,求证:函数f (x)在(1,+∞)上是增函数;
(Ⅱ)求函数f (x)在[1,e]上的最小值及相应的x值;
(Ⅲ)若当x∈[1,e]时,f (x)≤(a+2)x恒成立,求实数a的取值范围.
解:(1)当![]() 时,
时,![]() ,
,
当![]() ,
,![]() ,
,
故函数![]() 在
在![]() 上是增函数. …………3分
上是增函数. …………3分
(2)![]() ,
,
当![]() ,
,![]() .
.
若![]() ,
,![]() 在
在![]() 上非负(仅当
上非负(仅当![]() ,x=1时,
,x=1时,![]() ),
),
故函数![]() 在
在![]() 上是增函数,
上是增函数,
此时![]()
![]() .
.
若![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
此时![]() 是减函数;
是减函数;
当![]() 时,
时,![]() ,
,
此时![]() 是增函数.
是增函数.
故![]()
![]()
![]() .
.
若![]() ,
,![]() 在
在![]() 上非正(仅当
上非正(仅当![]() ,x=e时,
,x=e时,![]() ),
),
故函数![]() 在
在![]() 上是减函数,
上是减函数,
此时![]()
![]() .
.
综上可知,当![]() 时,
时,![]() 的最小值为1,相应的x值为1;
的最小值为1,相应的x值为1;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,
,
相应的x值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,相应的x值为
,相应的x值为![]() . …………9分
. …………9分
(3)不等式![]() ,
,
可化为![]() .
.
∵![]() , ∴
, ∴![]() 且等号不能同时取,
且等号不能同时取,
所以![]() ,即
,即![]() ,
,
因而![]() (
(![]() )
)
令![]() (
(![]() ),
),
又![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
从而![]() (仅当x=1时取等号),
(仅当x=1时取等号),
所以![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 的最大值为
的最大值为![]() ,
,
所以a的取值范围是![]() . ……14分
. ……14分

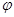 )(ω>0,0<
)(ω>0,0<
 =
= ,且a∈(0,
,且a∈(0, ),求f(a)的值.
),求f(a)的值. -a
-a +x(a>0).
+x(a>0). =
= ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程; 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.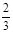 与x=1时都取得极值.
与x=1时都取得极值. ,若f(x)存在零点,则实数a的取值范围
,若f(x)存在零点,则实数a的取值范围