题目内容
设
是已知的平面向量且
≠
,关于向量
的分解,有如下四个命题:
①给定向量
,总存在向量
,使
=
+
;
②给定向量
和
,总存在实数λ和μ,使
=λ
+μ
;
③给定单位向量
和正数μ,总存在单位向量
和实数λ,使
=λ
+μ
;
④给定正数λ和μ,总存在单位向量
和单位向量
,使
=λ
+μ
;
上述命题中的向量
,
和
在同一平面内且两两不共线,则真命题的个数是( )
| a |
| a |
| 0 |
| a |
①给定向量
| b |
| c |
| a |
| b |
| c |
②给定向量
| b |
| c |
| a |
| b |
| c |
③给定单位向量
| b |
| c |
| a |
| b |
| c |
④给定正数λ和μ,总存在单位向量
| b |
| c |
| a |
| b |
| c |
上述命题中的向量
| b |
| c |
| a |
| A.1 | B.2 | C.3 | D.4 |
选项①,给定向量
和
,只需求得其向量差
-
即为所求的向量
,
故总存在向量
,使
=
+
,故①正确;
选项②,当向量
,
和
在同一平面内且两两不共线时,向量
,
可作基底,
由平面向量基本定理可知结论成立,故可知②正确;
选项③,由题意必有λ
和μ
表示不共线且长度不定的向量,
由于μ为正数,故λ
+μ
不能把向量任意
表示出来,故③错误;
选项④,因为λ和μ为正数,所以λ
和μ
代表与原向量同向的且有固定长度的向量,
这就使得向量
不一定能用两个单位向量的组合表示出来,
故不一定能使
=λ
+μ
成立,故④错误.
故选B
| a |
| b |
| a |
| b |
| c |
故总存在向量
| c |
| a |
| b |
| c |
选项②,当向量
| b |
| c |
| a |
| b |
| c |
由平面向量基本定理可知结论成立,故可知②正确;
选项③,由题意必有λ
| b |
| c |
由于μ为正数,故λ
| b |
| c |
| a |
选项④,因为λ和μ为正数,所以λ
| b |
| c |
这就使得向量
| a |
故不一定能使
| a |
| b |
| c |
故选B

练习册系列答案
相关题目
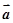 是已知的平面向量且
是已知的平面向量且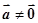 ,关于向量
,关于向量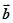 ,总存在向量
,总存在向量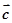 ,使
,使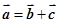 ;
; 和
和 ,使
,使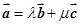 ;
;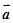 是已知的平面向量且
是已知的平面向量且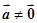 ,关于向量
,关于向量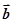 ,总存在向量
,总存在向量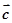 ,使
,使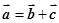 ;
;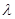 和
和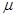 ,使
,使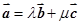 ;
;