Question

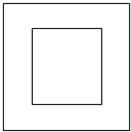
（1）在长16cm的线段AB上任取一点M，并以线段AM为边作正方形，则这个正方形的面积介于25cm²与81cm²之间的概率．
（2）如图所示，在一个边长为5cm的正方形内部画一个边长为3cm的正方形内随机投点，求所投的点落入大正方形内小正方形外的概率．

Answer 1

分析：（1）由题意可知，AM介于5cm与9cm之间，代入几何概率的计算公式可求；
（2）记“所投的点落入大正方形内小正方形外”为事件A，则“所投的点落入小正方形内”为事件A的对立事件

.

A

，所以P（A）=1-P（

.

A

）可求．

解答：解：（1）由题意可知，以线段AM为边长的正方形面积要介于25cm²与81cm²之间，
即要求AM介于5cm与9cm之间，
记“以线段AM为边长的正方形面积介于25cm²与81cm²之间”为事件A，
则由几何概型的求概率的公式得P（A）=

9-5

16

=

1

4

．
（2）记“所投的点落入大正方形内小正方形外”为事件A，
则“所投的点落入小正方形内”为事件A的对立事件

.

A

，
所以P（A）=1-P（

.

A

）=1-

32

52

=

16

25

点评：本题主要考查了与面积和长度有关的几何概率的概率公式的应用，要注意解题中对立事件在求解概率中的应用．