题目内容
设函数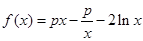 .
.
(1)若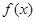 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数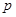 的取值范围;
的取值范围;
(2)设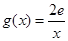 ,且
,且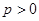 ,若在
,若在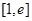 上至少存在一点
上至少存在一点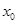 ,使得
,使得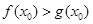 成立,求实数
成立,求实数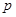 的取值范围.
的取值范围.
【答案】
(1)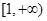 ;(2)
;(2)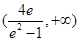 .
.
【解析】
试题分析:本题综合考查函数与导数及运用导数求单调区间、最值等数学知识和方法,考查函数思想、综合运用数学知识和方法分析问题解决问题的能力.第一问,属于恒成立问题,通过导数将单调性问题转化为求函数最值的问题,根据基本不等式求最值;第二问,属于存在性问题,构造函数转化为求函数最值问题,用导数判断函数的单调性求最值.
试题解析:(1) 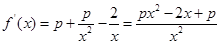 ,
,
依题意,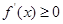 在
在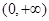 内恒成立,
内恒成立,
只需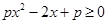 在
在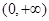 内恒成立
,
内恒成立
,
只需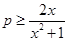 在
在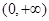 内恒成立,
内恒成立,
只需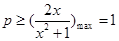 ,
,
故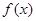 在其定义域内为单调递增函数时
在其定义域内为单调递增函数时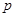 的取值范围是
的取值范围是 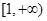 .(6分)
.(6分)
(2)依题意,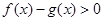 在
在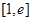 上有解
,
上有解
,
设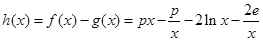 ,
,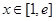 ,
,
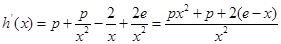 ,
,
因为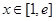 ,
,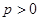 ,所以
,所以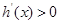 在
在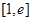 上恒成立,
上恒成立,
所以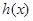 在
在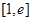 上是增函数,所以
上是增函数,所以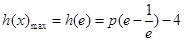 ,依题意,要
,依题意,要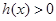 在
在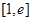 上有解,只需
上有解,只需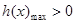 ,
,
所以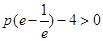 ,解得
,解得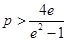 ,
,
故所求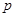 的取值范围是
的取值范围是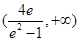 .(12分)
.(12分)
考点:1.恒成立问题;2.函数最值;3.存在性问题;4.判断函数的单调性.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
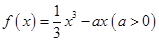 ,
,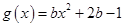 .
.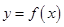 与
与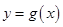 在它们的交点
在它们的交点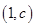 处有相同的切线,求实数
处有相同的切线,求实数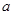 、
、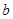 的值;
的值;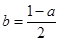 时,若函数
时,若函数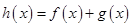 在区间
在区间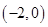 内恰有两个零点,求实数
内恰有两个零点,求实数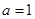 ,
,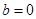 时,求函数
时,求函数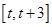 上的最小值.
上的最小值.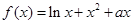 。
。 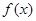 在
在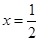 处取得极值,求
处取得极值,求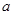 的值;
的值;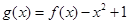 ,当
,当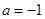 时,
时,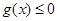 在其定义域内恒成立;
在其定义域内恒成立;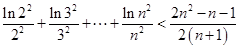 。
。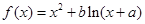 ,其中
,其中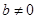 。
。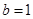 时,
时,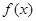 在
在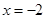 时取得极值,求
时取得极值,求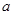 ;
;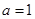 时,若
时,若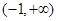 上单调递增,求
上单调递增,求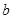 的取值范围;
的取值范围;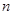 ,不等式
,不等式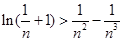 都成立。
都成立。