题目内容
已知矩阵A=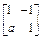
，其中a∈R，若点P（1，1）在矩阵A的变换下得到点P′（0，-3）.（1）求实数a的值；
（2）求矩阵A的特征值及特征向量.
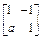，其中a∈R，若点P（1，1）在矩阵A的变换下得到点P′（0，-3）.（1）求实数a的值；（2）求矩阵A的特征值及特征向量.
（1）-4（2）矩阵A的属于特征值3的一个特征向量为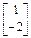
.矩阵A的属于特征值-1的一个特征向量为
.
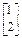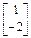.矩阵A的属于特征值-1的一个特征向量为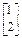.（1）由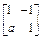
=
得a+1=-3
a=-4.
（2）由（1）知A=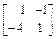
则矩阵A的特征多项式为
f（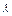
）=
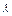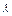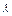=（-1）2-4=2-2-3
令f(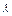)=0,得矩阵A的特征值为-1或3.
设矩阵A的特征向量为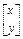
当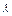=-1时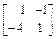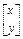，="(-1)"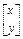
即
,所以y=2x.
∴矩阵A的属于特征值-1的一个特征向量为
.
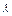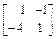
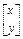当=3时，=3,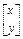
即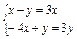
,所以2x+y=0.
∴矩阵A的属于特征值3的一个特征向量为
.
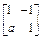
=得a+1=-3
a=-4.（2）由（1）知A=
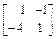
则矩阵A的特征多项式为
f（
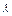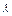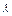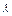）==（-1）2-4=2-2-3令f(
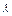)=0,得矩阵A的特征值为-1或3.设矩阵A的特征向量为
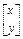
当
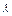=-1时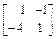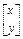，="(-1)"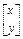 即
,所以y=2x.∴矩阵A的属于特征值-1的一个特征向量为
.当
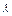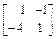
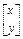=3时，=3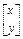,即
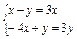,所以2x+y=0.∴矩阵A的属于特征值3的一个特征向量为
.
练习册系列答案
阅读快车系列答案
相关题目
的矩
。若
，求（1）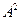
，
；
，并用数学归纳法证明。
，其中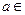
R，若点P（1，1）在矩阵A的变换下得到点P′（0，－3），求矩阵A的特征值及特征向量．
已知二阶矩阵A的属于特征值－1的一个特征向量为，属于特征值3的一个特征向量为，求矩阵A．
化成四进位制数的末位是____________。 
,则
( )