题目内容
已知S={θ|f(x)=cosω(x+θ)(ω∈N+)是奇函数},P={x|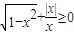 },若S∩P=∅,则ω是 .
},若S∩P=∅,则ω是 .
【答案】分析:先根据f(x)=cosω(x+θ)(ω∈N+)是奇函数得出:f(0)=0,进一步得到θ=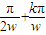 ,(k∈Z,ω∈N+)又P={x|
,(k∈Z,ω∈N+)又P={x|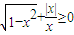 }={x|-1≤<0或0<x≤1},为了保证S∩P=∅,从而只有ω=1,从而解决问题.
}={x|-1≤<0或0<x≤1},为了保证S∩P=∅,从而只有ω=1,从而解决问题.
解答:解:∵f(x)=cosω(x+θ)(ω∈N+)是奇函数
∴f(0)=0,得cosω(0+θ)=0,
∴θ=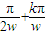 ,(k∈Z,ω∈N+)
,(k∈Z,ω∈N+)
又P={x|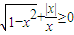 }={x|-1≤<0或0<x≤1},
}={x|-1≤<0或0<x≤1},
若S∩P=∅,
则ω=1,否则S与P有公共元素,
故答案为:1
点评:本小题主要考查余弦函数的奇偶性、交集及其运算、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
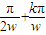 ,(k∈Z,ω∈N+)又P={x|
,(k∈Z,ω∈N+)又P={x|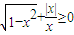 }={x|-1≤<0或0<x≤1},为了保证S∩P=∅,从而只有ω=1,从而解决问题.
}={x|-1≤<0或0<x≤1},为了保证S∩P=∅,从而只有ω=1,从而解决问题.解答:解:∵f(x)=cosω(x+θ)(ω∈N+)是奇函数
∴f(0)=0,得cosω(0+θ)=0,
∴θ=
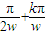 ,(k∈Z,ω∈N+)
,(k∈Z,ω∈N+)又P={x|
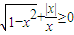 }={x|-1≤<0或0<x≤1},
}={x|-1≤<0或0<x≤1},若S∩P=∅,
则ω=1,否则S与P有公共元素,
故答案为:1
点评:本小题主要考查余弦函数的奇偶性、交集及其运算、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
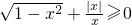 },若S∩P=∅,则ω是________.
},若S∩P=∅,则ω是________.