题目内容
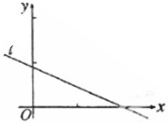设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（ ）| A、x和y的相关系数为直线l的斜率 | ||||
| B、x和y的相关系数在0到1之间 | ||||
| C、当n为偶数时，分布在l两侧的样本点的个数一定相同 | ||||
D、直线l过点（
|
分析：对于所给的线性回归方程对应的直线，针对于直线的特点，回归直线一定通过这组数据的样本中心点，得到结果．
解答：解：直线l是由这些样本点通过最小二乘法得到的线性回归直线，
回归直线方程一定过样本中心点，
故选D．
回归直线方程一定过样本中心点，
故选D．
点评：本题考查线性回归方程的性质，考查样本中心点一定在回归直线上，本题是一个基础题，不需要运算就可以看出结果．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
设
=(x1，y1)，
=(x2，y2)，若|
|=2，|
|=3，
•
=-6，则
=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n次方个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论正确的是（ ）A、直线l过点(
| ||||
| B、x和y的相关系数为直线l的斜率 | ||||
| C、x和y的相关系数在0到1之间 | ||||
| D、当n为偶数时，分布在l两侧的样本点的个数一定相同 |
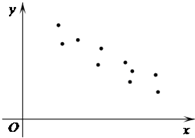设（x1，y1），（x2，y2），…，（xn，yn），是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归方程（如图），以下结论中正确的是（ ）| A、x和y正相关 | B、x和y的相关系数为直线l的斜率 | C、x和y的相关系数在-1到0之间 | D、当n为偶数时，分布在l两侧的样本点的个数一定相同 |