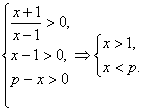Question

设f(x)=log₂+log₂(x－1)+log₂(p－x)，

（1）求函数f(x)的定义域；

（2）f(x)是否存在最大值或最小值？如果存在，请把它求出来；如果不存在，请说明理由。

 

Answer 1

答案：
解析：

（1）三个对数式都要有意义，则有定义域不能是空集，故p>1，从而知函数的定义域为（1，p）。 （2）下面是在函数的定义域内考虑函数的最值问题，函数式可化成 f(x)=log2(x+1)(p－x)=log2[－x2+(p－1)x+p]=log2[－(x－)2+]. 容易验证：1<<p， 即∈(1，p).∴当x=时，函数有最大值f(x)max=log2.显然函数没有最小值。其原因是二次函数－（x－）2+在（1，p）上无最小值。