题目内容
已知△ABC的面积为2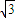
，AB=2，BC=4，则三角形的外接圆半径为 ．
【答案】分析：利用三角形的面积公式求出B的大小，然后判断三角形的形状，利用余弦定理求出第三边的长，通过正弦定理求出外接圆的半径即可．
解答：解：根据面积为2
=
AB•BCsinB=4sinB，∴sinB=
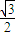，∴B=60°．或B=120°．
当B=60°时，三角形是直角三角形，外接圆的半径为：2；
当B=120°时，三角形的第三边为：
=4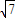
．
所以三角形的外接圆的半径为：
=
．
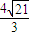故答案为：2或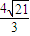
．
点评：本题考查余弦定理的应用，正弦定理的应用，三角形的面积公式的应用，考查计算能力转化思想．
解答：解：根据面积为2
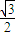=AB•BCsinB=4sinB，∴sinB=，∴B=60°．或B=120°．当B=60°时，三角形是直角三角形，外接圆的半径为：2；
当B=120°时，三角形的第三边为：
=4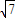．所以三角形的外接圆的半径为：
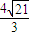=．故答案为：2或
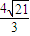．点评：本题考查余弦定理的应用，正弦定理的应用，三角形的面积公式的应用，考查计算能力转化思想．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使
（2012•温州一模）如图，在△ABC中，AD⊥BC，垂足为D，且BD：DC：AD=2：3：6．