题目内容
过双曲线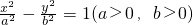 的左焦点,且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于
的左焦点,且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于
- A.3
- B.

- C.2
- D.

C
分析:先求出当x=-c时,y的值,再利用以MN为直径的圆恰好过双曲线的右顶点,建立方程,由此可得双曲线的离心率.
解答:由题意,当x=-c时,y=±
∵以MN为直径的圆恰好过双曲线的右顶点,
∴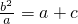
∴c2-a2=a(a+c)
∴c-a=a
∴c=2a
∴e=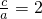
故选C.
点评:本题考查双曲线的几何性质,考查学生的计算能力,属于基础题.
分析:先求出当x=-c时,y的值,再利用以MN为直径的圆恰好过双曲线的右顶点,建立方程,由此可得双曲线的离心率.
解答:由题意,当x=-c时,y=±

∵以MN为直径的圆恰好过双曲线的右顶点,
∴
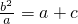
∴c2-a2=a(a+c)
∴c-a=a
∴c=2a
∴e=
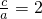
故选C.
点评:本题考查双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
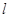 过双曲线的左焦点
过双曲线的左焦点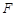 ,且与以实轴为直径的圆相切,若直线
,且与以实轴为直径的圆相切,若直线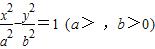 的左焦点,且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于( )
的左焦点,且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于( )
