题目内容
由2开始的偶数数列,按下列方法分组:(2),(4,6),(8,10,12),…,第n组有n个数,则第n组的首项为( )
分析:设第n组的首项为an,由题中数列的规律可得a2-a1=2,a3-a2=4,a4-a3=6,…,an-an-1=2(n-1).由此结合题中数据利用等差数列求和公式,即可算出an的通项公式,从而得出第n组的首项.
解答:解:根据题意,可得如图的三角形数阵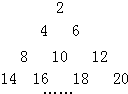
记每一行的第一个数为an,得
a1=2,a2=4,a3=8,a4=14,…
发现如下规律:
a2-a1=2,a3-a2=4,a4-a3=6,…,an-an-1=2(n-1)
将此n-1个式子相加,得
an-a1=2[1+2+3+…+(n-1)]=2×
=n2-n,
∴an=a1+(n2-n)=n2-n+2,即第n组的首项为n2-n+2
故选:D

记每一行的第一个数为an,得
a1=2,a2=4,a3=8,a4=14,…
发现如下规律:
a2-a1=2,a3-a2=4,a4-a3=6,…,an-an-1=2(n-1)
将此n-1个式子相加,得
an-a1=2[1+2+3+…+(n-1)]=2×
| n(n-1) |
| 2 |
∴an=a1+(n2-n)=n2-n+2,即第n组的首项为n2-n+2
故选:D
点评:本题给出数列实际应用问题,求第n组的首项.着重考查了等差数列的通项公式、求和公式和归纳推理的一般方法等知识,属于中档题.

练习册系列答案
相关题目