题目内容
已知二次函数![]() 对任意
对任意![]() 都有
都有![]() <0且
<0且![]() =
=![]() 成立,设向量
成立,设向量
![]() ,b=(2sin
,b=(2sin![]() ,
,![]() ),c=(
),c=(![]() ,1),d=(1,2),当
,1),d=(1,2),当![]() 是三角形内角时,求不等式
是三角形内角时,求不等式![]() (
(![]() ?b)>
?b)>![]() (c?d)的解集.
(c?d)的解集.
解:∵![]() =
=![]() ,
,
∴![]() 的图像关于直线
的图像关于直线![]() =1对称;
=1对称;
∵二次函数![]() 对任意
对任意![]() ∈R都有
∈R都有![]() <0,所以二次函数的图像必开口向下,
<0,所以二次函数的图像必开口向下,
∴![]() ≥1时,
≥1时,![]() 是减函数.
是减函数.
∵![]() =
=![]() ?(2sin
?(2sin![]() ,
,![]() )=2sin2
)=2sin2![]() +1≥1,
+1≥1,
c?d=(cos2![]() ,1)?(1,2)=cos2
,1)?(1,2)=cos2![]() +2≥1,
+2≥1,
∴![]() (
(![]() ?b)>
?b)>![]() (c?d)
(c?d)
![]()
![]() (2sin2
(2sin2![]() +1)>
+1)>![]() (cos2
(cos2![]() +2)
+2)
![]() 2sin2
2sin2![]() +1<cos2
+1<cos2![]() +2
+2
![]() 1一cos2
1一cos2![]() +1<cos2
+1<cos2![]() +2
+2
![]() cos2
cos2![]() >0
>0
=>![]()
又∵0<![]() <
<![]() ∴0<
∴0<![]() <
<![]() 或
或![]() <
<![]() <
<![]() ,
,
![]() (
(![]() ?b)>
?b)>![]() (c?d)的解集是{
(c?d)的解集是{![]() |0<
|0<![]() <
<![]() 或
或![]() <
<![]() <
<![]() }.
}.

练习册系列答案
相关题目
 对任意实数
对任意实数 都满足
都满足 且
且
 求证:
求证: 上为减函数;
上为减函数; ,恒有
,恒有
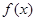 对任意
对任意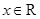 ,都有
,都有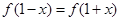 成立,设向量
成立,设向量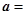 (sinx,2),
(sinx,2),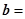 (2sinx,
(2sinx,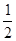 ),
),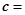 (cos2x,1),
(cos2x,1),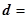 (1,2),当
(1,2),当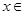 [0,
[0,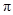 ]时,求不等式f(
]时,求不等式f(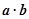 )>f(
)>f(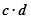 )的解集.
)的解集.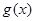 对任意实数
对任意实数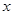 都满足
都满足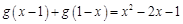 ,且
,且 .令
.令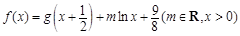 .
.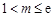 ,
,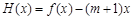 ,证明:对任意
,证明:对任意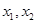
 ,恒有
,恒有
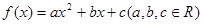 对任意实数
对任意实数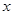 ,都有
,都有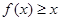 ,且
,且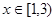 时,有
时,有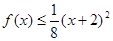 成立,(1)证明f(2)=2;(2)若
成立,(1)证明f(2)=2;(2)若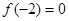 ,求f(x)的表达式;⑶ 在题(2)的条件下设
,求f(x)的表达式;⑶ 在题(2)的条件下设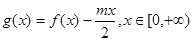 ,若
,若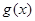 图象上的点都位于直线
图象上的点都位于直线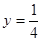 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.