题目内容
设a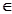 R,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________.
R,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________.
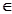 R,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________.
R,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________.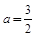
解:(1)a=1时,代入题中不等式明显不成立.
(2)a≠1,构造函数y1=(a-1)x-1,y2=x 2-ax-1,它们都过定点P(0,-1).
考查函数y1=(a-1)x-1:令y=0,得M(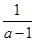 ,0),
,0),
∴a>1;
考查函数y2=x 2-ax-1,显然过点M(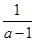 ,0),代入得:(
,0),代入得:(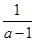 )2?
)2?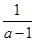 ?1=0,
?1=0,
解之得:a= ,或a=0(舍去).
,或a=0(舍去).
故答案为:
(2)a≠1,构造函数y1=(a-1)x-1,y2=x 2-ax-1,它们都过定点P(0,-1).
考查函数y1=(a-1)x-1:令y=0,得M(
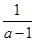 ,0),
,0),∴a>1;
考查函数y2=x 2-ax-1,显然过点M(
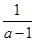 ,0),代入得:(
,0),代入得:(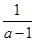 )2?
)2?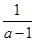 ?1=0,
?1=0,解之得:a=
 ,或a=0(舍去).
,或a=0(舍去).故答案为:


练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
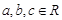 ,且
,且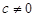 ,则下列命题正确的是( )
,则下列命题正确的是( ) ,那么
,那么
 ,那么
,那么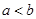

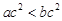 ,那么
,那么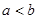 ,则下列不等式成立的是
,则下列不等式成立的是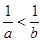
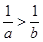
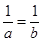
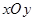 中,圆
中,圆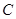 的参数方程为
的参数方程为
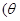 为参数,
为参数,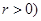 .以
.以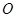 为极点,
为极点,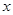 轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线
轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线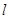 的极坐标方程为
的极坐标方程为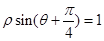 .当圆
.当圆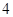 时,圆的半径
时,圆的半径 .
.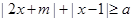 恒成立时,若实数
恒成立时,若实数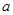 的最大值为3,则实数
的最大值为3,则实数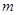 的值为 .
的值为 .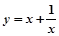
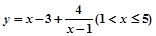
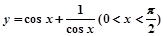
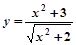
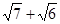
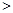
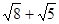 ,分析其结构,请你再写出一个不等式,使以上不等式为它的特殊情况。若
,分析其结构,请你再写出一个不等式,使以上不等式为它的特殊情况。若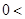
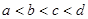 ,且
,且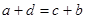 则该不等式可以是 .
则该不等式可以是 .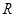 的函数
的函数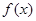 满足:
满足: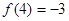 ,且对任意
,且对任意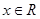 总有
总有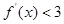 ,则不等式
,则不等式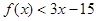 的解集为( )
的解集为( ) 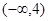

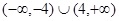
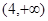
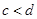 ,
, 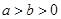 , 下列不等式中必然成立的一个是( )
, 下列不等式中必然成立的一个是( )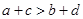
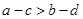
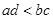

 ,
, ,则下列有关
,则下列有关 与
与 的大小关系表述正确的是______
的大小关系表述正确的是______ ; ②
; ② ; ③
; ③ (填正确的序号).
(填正确的序号).