题目内容
已知集合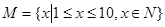 ,对它的非空子集A,将A中每个元素k,都乘以
,对它的非空子集A,将A中每个元素k,都乘以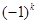 再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对
再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对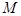 的所有非空子集,这些和的总和是 .
的所有非空子集,这些和的总和是 .
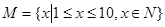 ,对它的非空子集A,将A中每个元素k,都乘以
,对它的非空子集A,将A中每个元素k,都乘以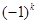 再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对
再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对 的所有非空子集,这些和的总和是 .
的所有非空子集,这些和的总和是 . 2560;
解:∵M={x|1≤x≤10,x∈N}={1,2,…10},
∴M中所有非空子集中含有1的有10类:
①单元素集合只有{1}含有1,即1出现了C90次;
②双元素集合有1的有{1,2},{1,3},…{1,10},即1出现了C91次;
③三元素集合中含有1的有{1,2,3},{1,2,4},…{1,9,10}即1出现了C92次;
…
⑩含有十个元素{1,2,…}1出现了C99次;
∴1共出现
同理2,3,4,…10各出现29次,
∴M的所有非空子集中,这些和的总和是 29•[(-1)1+2×(-1)2+…+10×(-1)10]=29×5=2560.
故答案为:2560.
∴M中所有非空子集中含有1的有10类:
①单元素集合只有{1}含有1,即1出现了C90次;
②双元素集合有1的有{1,2},{1,3},…{1,10},即1出现了C91次;
③三元素集合中含有1的有{1,2,3},{1,2,4},…{1,9,10}即1出现了C92次;
…
⑩含有十个元素{1,2,…}1出现了C99次;
∴1共出现

同理2,3,4,…10各出现29次,
∴M的所有非空子集中,这些和的总和是 29•[(-1)1+2×(-1)2+…+10×(-1)10]=29×5=2560.
故答案为:2560.

练习册系列答案
相关题目
 ,集合
,集合 ,集合
,集合 ,若
,若 中含有两个元素,则a的取值为( )
中含有两个元素,则a的取值为( )
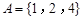 ,
,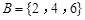 ,则
,则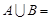 ▲ .
▲ .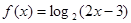 的定义域为集合
的定义域为集合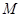 ,函数
,函数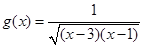 的定义域为集合
的定义域为集合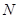 .求:
.求: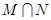 ,
,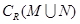 .
.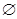
 ,集合
,集合 ,
, ,则
,则 =( )
=( )



 ,
,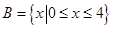 ,则
,则 .
. 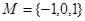 ,
,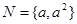 则使M∩N=N成立的
则使M∩N=N成立的 的值是( )
的值是( )