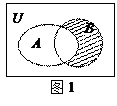题目内容
(本题满分14分,第(1)小题6分,第(2)小题8分)
设全集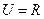 ,关于
,关于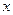 的不等式
的不等式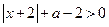 (
(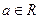 )的解集为
)的解集为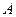 .
.
(1)分别求出当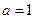 和
和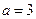 时的集合
时的集合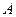 ;
;
(2)设集合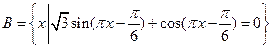 ,若
,若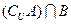 中有且只有三个元素,求实数
中有且只有三个元素,求实数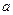 的取值范围.
的取值范围.
设全集
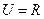 ,关于
,关于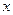 的不等式
的不等式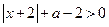 (
(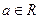 )的解集为
)的解集为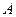 .
.(1)分别求出当
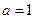 和
和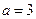 时的集合
时的集合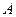 ;
;(2)设集合
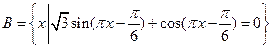 ,若
,若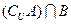 中有且只有三个元素,求实数
中有且只有三个元素,求实数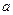 的取值范围.
的取值范围.(Ⅰ) 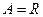 (Ⅱ)
(Ⅱ) 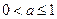
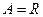 (Ⅱ)
(Ⅱ) 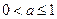
(1)当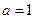 时,
时,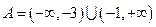 …………………3分
…………………3分
当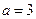 时,
时,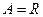 ………………………………………………………6分
………………………………………………………6分
(2)由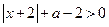 可以得到:
可以得到: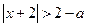 .
.
当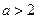 ,解集是
,解集是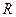 ;
;
当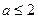 时,解集是
时,解集是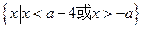 ………………………………8分
………………………………8分
(i)当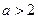 时,
时,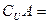
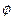 ,不合题意;
,不合题意;
(ii)当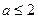 时,
时,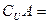
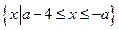 ………………………………10分
………………………………10分
因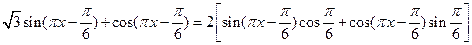
=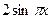
由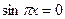 ,得
,得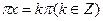 ,即
,即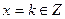 ,所以
,所以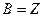 ……………12分
……………12分
当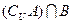 有3个元素时,
有3个元素时,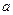 就满足
就满足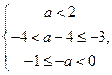
可以得到: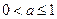 ………………………………………………14分
………………………………………………14分
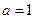 时,
时,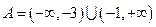 …………………3分
…………………3分当
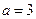 时,
时,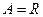 ………………………………………………………6分
………………………………………………………6分(2)由
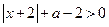 可以得到:
可以得到: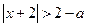 .
.当
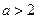 ,解集是
,解集是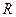 ;
;当
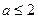 时,解集是
时,解集是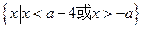 ………………………………8分
………………………………8分(i)当
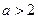 时,
时,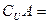
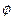 ,不合题意;
,不合题意;(ii)当
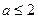 时,
时,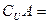
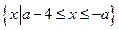 ………………………………10分
………………………………10分因
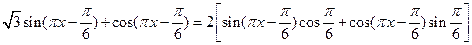
=
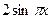
由
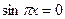 ,得
,得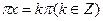 ,即
,即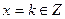 ,所以
,所以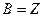 ……………12分
……………12分当
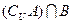 有3个元素时,
有3个元素时,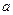 就满足
就满足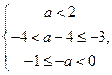
可以得到:
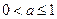 ………………………………………………14分
………………………………………………14分
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
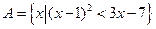 ,则
,则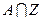 的元素个数为 。
的元素个数为 。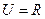 ,集合
,集合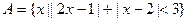 ,
,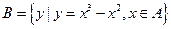 ,求
,求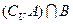
 ,那么使
,那么使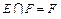 成立的充要条件是( )
成立的充要条件是( )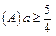
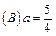
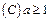
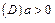
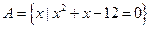 ,
,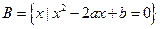 ,问是否存在实数
,问是否存在实数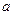 、
、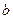 ,使
,使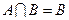 ,若存在,求出
,若存在,求出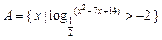 ,
,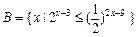 ,求
,求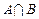 .
.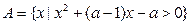 ,
,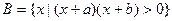 ,其中
,其中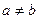 ,集合
,集合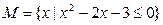 ,全集
,全集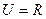 。
。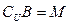 ,求
,求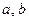 的值;
的值;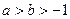 ,求
,求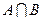 。
。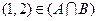 ,集合
,集合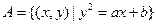 ,
,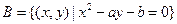 ,则
,则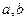 的值( ).
的值( ).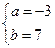
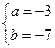
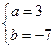
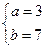
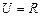 ,集合
,集合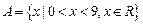 和
和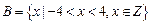 关系的韦恩图如图1所示,则阴影部分所示集合中的元素共有
关系的韦恩图如图1所示,则阴影部分所示集合中的元素共有