题目内容
在三棱柱 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱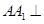 底面
底面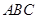 ,点
,点 是侧面
是侧面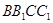 的中心,若
的中心,若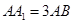 ,则直线
,则直线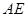 与平面
与平面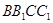 所成角的大小为( )
所成角的大小为( )
A.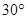 B.
B. C.
C.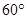 D.
D.
【答案】
A
【解析】
试题分析:由题意画出图形,取BC的中点D,连接AD与ED,因为三棱柱ABC-A1B1C1中,底面是正三角形,侧棱AA1⊥底面ABC,所以平面BCC1B1⊥平面ABC,点E是侧面BB1CC1的中心,所以ED⊥BC,AD⊥BC,所以AD⊥平面EBC,∠AED就是直线AE与平面BB1CC1所成角,∵AA1=3AB,∴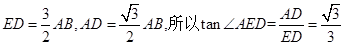 ,所以∠AED=30°,即直线
,所以∠AED=30°,即直线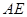 与平面
与平面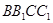 所成角
所成角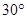 。
。
考点:直线与平面所成的角;正棱柱的结构特征。
点评:本题考查直线与平面垂直的判断方法,直线与平面所成角的求法,考查计算能力.

练习册系列答案
相关题目

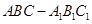 中,底面边长为
中,底面边长为 ,侧棱长为
,侧棱长为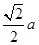 ,
,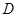 是棱
是棱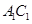 的中点.
的中点.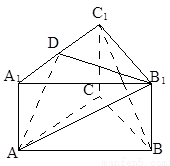
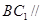 平面
平面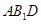 ;
;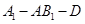 的大小;
的大小;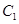 到平面
到平面 中,底面边长为
中,底面边长为 ,侧棱长为
,侧棱长为 ,
, 是棱
是棱 的中点.
的中点. 
 平面
平面 ;
;
 的大小;
的大小; 到平面
到平面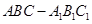 中,底面边长为
中,底面边长为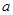 ,侧棱长为
,侧棱长为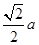 ,
,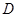 是棱
是棱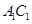 的中点.
的中点. 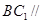 平面
平面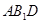 ;
;
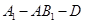 的大小;[来源:ZXXK]
的大小;[来源:ZXXK]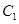 到平面
到平面