题目内容
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2,且∠A1AD=∠A1AB=60°,AC与BC交于点O.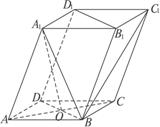
(1)求证:A1O⊥平面ABCD;
(2)求BC1与底面ABCD所成的角;
(3)求侧棱AA1和截面B1D1DB的距离.
(1)证明:连结A1D、A1B,
由已知可得△AA1B和△A1AD为全等的正三角形.
∴A1B=A1D1,
∴A1O⊥BD.
又AB=AD,BD=BD,∴△ABD≌△A1BD,A1O=AO=![]() ,
,
又AA1=2,∴A1O⊥AO,
∴A1O⊥平面ABCD.
(2)解:过C1作C1H⊥AC交AC的延长线于H,则C1H⊥平面ABCD,
连结BH,则∠C1BH为BC1与平面ABCD所成的角.
∵OH=A1C1=![]() ,BO=
,BO=![]() ,
,
∴BH=![]() .
.
∴tanC1BH=![]() ,
,
∴∠C1BH=arctan![]() .
.
((2)也可用向量法求解)
(3)解:连结OO1,易知AA1∥OO1,面AA1O1O⊥面BDD1B1,
作A1G⊥OO1,则A1G为AA1与面B1D1DB的距离.由(1)知A1O=AO=A1O1,A1O⊥A1O1,∴A1G=![]() OO1=1
OO1=1
((3)也可用向量法或等积法求解).

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
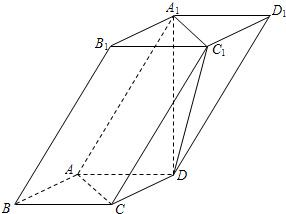 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.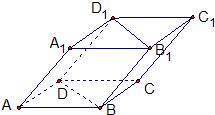 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是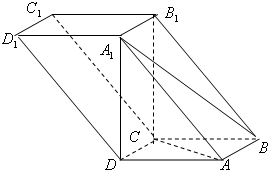 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,