题目内容
求函数![]() 的单调区间与极值。
的单调区间与极值。
![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 和
和![]() 上递减,当
上递减,当![]() 时函数取得极小值
时函数取得极小值![]() ,当
,当![]() 时,函数取得极大值
时,函数取得极大值![]() 。
。
解析:
![]() ,由
,由![]() 得
得![]() 或
或![]() 或
或![]() ,这三点把
,这三点把![]() 分成四个单调区间,我们列表如下:
分成四个单调区间,我们列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 递减 | 极小值 | 递增 | 极大值 | 递减 | 极小值 | 递增 |
∴![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 和
和![]() 上递减,当
上递减,当![]() 时函数取得极小值
时函数取得极小值![]() ,当
,当![]() 时,函数取得极大值
时,函数取得极大值![]() 。
。

练习册系列答案
相关题目
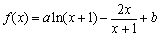 的图象与直线
的图象与直线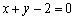 相切于点
相切于点 .
.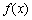 的单调区间和极小值.
的单调区间和极小值.