题目内容
方程sin
=logax(a>0且a≠1)恰有三个不相等的实数根,则( )
| πx |
| 2 |
分析:在同一坐标系里作出函数f(x)=sin(
x)和g(x)=logax的图象,讨论当a>1时图象交点的个数,可得当a∈(5,7)时,两图象恰有三个公共点;当0<a<1时,同理可得在a∈(
,
,)时,两图象恰有三个公共点.由此可得本题的正确答案.
| π |
| 2 |
| 1 |
| 7 |
| 1 |
| 3 |
解答:解:记f(x)=sin(
x)和g(x)=logax,方程sin
=logax(a>0且a≠1)恰有三个不相等的实数根,
可以理解为函数f(x)的图象g(x)恰有三个公共点.
作出两个函数的图象如下:
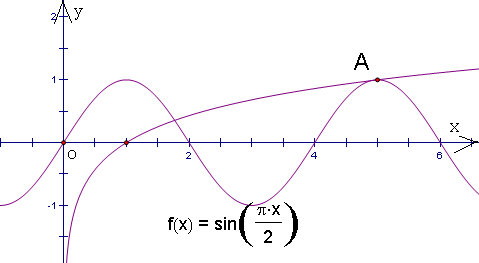
当a>1时,在a=5的情况下,对数函数y=g(x)恰好经过函数三角y=f(x)的y轴右侧的最大值点A(5,1),此时两个图象恰好有两个公共点;而当在a=9的情况下,对数函数y=g(x)恰好经过函数三角y=f(x)的y轴右侧的最大值点A(9,1),此时两个图象恰好有4个公共点;说明只有5<a<9时,两个函数图象的公共点的个数恰好为3个.
当0<a<1时,同样的方法可得,在a∈(
,
,)时,两图象恰有三个公共点.
故原方程恰有3个实数根时,a∈(
,
)∪(5,9)
故选D
| π |
| 2 |
| πx |
| 2 |
可以理解为函数f(x)的图象g(x)恰有三个公共点.
作出两个函数的图象如下:

当a>1时,在a=5的情况下,对数函数y=g(x)恰好经过函数三角y=f(x)的y轴右侧的最大值点A(5,1),此时两个图象恰好有两个公共点;而当在a=9的情况下,对数函数y=g(x)恰好经过函数三角y=f(x)的y轴右侧的最大值点A(9,1),此时两个图象恰好有4个公共点;说明只有5<a<9时,两个函数图象的公共点的个数恰好为3个.
当0<a<1时,同样的方法可得,在a∈(
| 1 |
| 7 |
| 1 |
| 3 |
故原方程恰有3个实数根时,a∈(
| 1 |
| 7 |
| 1 |
| 3 |
故选D
点评:本题以三角函数和对数函数为例,考查了函数零点与方程根的个数的讨论等知识点,属于中档题.采用数形结合法,找图象上的界点,从而找到实数a的临界值,是解决本题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
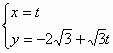 (t为参数)
(t为参数)