题目内容
已知平面上两定点C(-1,0),D(1,0)和一定直线l:x=-4,P为该平面上一动点,作PQ⊥l,垂足为Q,且(| PQ |
| PC |
| PQ |
| PC |
(1)问点P在什么曲线上,并求出曲线的轨迹方程M;
(2)又已知点A为抛物线y2=2px(p>0)上一点,直线DA与曲线M的交点B不在y轴的右侧,且点B不在x轴上,并满足
| AB |
| DA |
分析:(1)先由(
+2
)(
-2
)=0.得|
|=2|
|.法一:转化为到定点的距离和到定直线的距离问题即椭圆定义,就可求出点P所在曲线以及曲线的轨迹方程M;
法二:直接设出点P的坐标,代入整理即可求出点P所在曲线以及曲线的轨迹方程M;
(2)先把点B的坐标设出来,利用
=2
求出点A的坐标,再利用点A为抛物线y2=2px(p>0)上一点,求出p和点B的坐标之间的关系,最后利用点B所在位置的限制求出p的最小值即可.
| PQ |
| PC |
| PQ |
| PC |
| PQ |
| PC |
法二:直接设出点P的坐标,代入整理即可求出点P所在曲线以及曲线的轨迹方程M;
(2)先把点B的坐标设出来,利用
| AB |
| DA |
解答: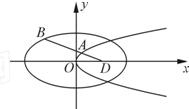 解:(1)由(
解:(1)由(
+2
)(
-2
)=0.得|
|=2|
|.
法一:动点P到定点C(-1,0)的距离与到定直线l:x=-4的距离之比为常数,
所以点P在椭圆上.
由
?a=2,b=
,c=1.
所以所求的椭圆方程为
+
=1.
法二:设P(x,y)代入|
|=2|
|.得点P的轨迹方程为
+
=1.
(2)椭圆的右焦点为D(1,0),点B在椭圆
+
=1(-2<x≤0)上,设B(x0,y0),其中-2<x0≤0
由
=2
,知xA=
,yA=
.
由点A在抛物线y2=2px上,得
=2p•
.
又
=1-
,∴8p=
.
令t=x0+2,则0<t≤2,
即8p=
=-t+4,∵0<t≤2∴当t=2时p最小
∴p=
,又当t=2时,x0=0为椭圆与y轴的交点.
故p的最小值为
 解:(1)由(
解:(1)由(| PQ |
| PC |
| PQ |
| PC |
| PQ |
| PC |
法一:动点P到定点C(-1,0)的距离与到定直线l:x=-4的距离之比为常数,
所以点P在椭圆上.
由
|
| 3 |
所以所求的椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
法二:设P(x,y)代入|
| PQ |
| PC |
| x2 |
| 4 |
| y2 |
| 3 |
(2)椭圆的右焦点为D(1,0),点B在椭圆
| x2 |
| 4 |
| y2 |
| 3 |
由
| AB |
| DA |
| x0+2 |
| 3 |
| y0 |
| 3 |
由点A在抛物线y2=2px上,得
| ||
| 9 |
| x0+2 |
| 3 |
又
| ||
| 3 |
| ||
| 4 |
4-
| ||
| x0+2 |
令t=x0+2,则0<t≤2,
即8p=
| -t2+4t |
| t |
∴p=
| 1 |
| 4 |
故p的最小值为
| 1 |
| 4 |
点评:本题综合考查了椭圆的定义,直线与抛物线的位置关系以及向量共线问题.是一道综合性很强的好题.

练习册系列答案
相关题目
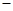 1,0),D(1,0)和一定直线
1,0),D(1,0)和一定直线 ,
, 为该平面上一动点,作
为该平面上一动点,作 ,垂足为Q,且
,垂足为Q,且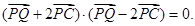
 上一点,直线DA与曲线M的交点B不在
上一点,直线DA与曲线M的交点B不在 轴的右侧,且点B不在
轴的右侧,且点B不在 轴上,并满足
轴上,并满足 的最小值.[来源:学
的最小值.[来源:学 .
.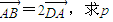 的最小值.
的最小值. 1,0),D(1,0)和一定直线
1,0),D(1,0)和一定直线 ,
, 为该平面上一动点,作
为该平面上一动点,作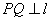 ,垂足为Q,且
,垂足为Q,且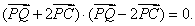
 上一点,直线DA与曲线M的交点B不在
上一点,直线DA与曲线M的交点B不在 轴的右侧,且点B不在
轴的右侧,且点B不在 轴上,并满足
轴上,并满足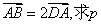 的最小值.
的最小值.