题目内容
下列函数中，对于任意的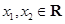
，满足条件
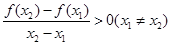的函数是（ ）
A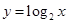． | B． | C． | D． |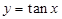
C
解析试题分析：由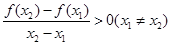可得函数
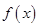在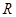
上单调递增。A、B、D三个选项中的函数定义域均不为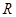，故舍。而在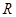上是增函数。故C正确。
考点：1单调性的定义；2函数的定义域及单调性。
练习册系列答案
寒假学与练系列答案
相关题目
已知函数
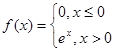，则使函数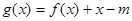
有零点的实数
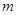的取值范围是（ ）
A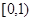． | B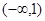． | C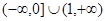． | D． |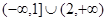
函数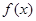
的部分图像如图所示，则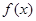的解析式可以是( )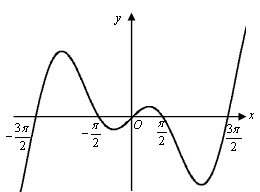
A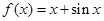． | B． |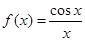
C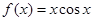． | D． |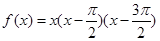
（2013•重庆）函数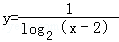
的定义域为（ ）
| A．（﹣∞，2） | B．（2，+∞） |
| C．（2，3）∪（3，+∞） | D．（2，4）∪（4，+∞） |
已知a>1，f(x)＝ax ＋2x，则使f(x)<1成立的一个充分不必要条件是 ( )
| A．－1<x<0 | B．－2<x<1 |
| C．－2<x<0 | D．0<x<1 |
若函数f(x)=|4x-x2|-a的零点个数为4，则a的取值范围是（ ）
| A．[0,3] | B．(0，4） | C．[-1,2] | D．(-1,4) |
（2013•浙江）已知a、b、c∈R，函数f（x）=ax2+bx+c．若f（0）=f（4）＞f（1），则（ ）
| A．a＞0，4a+b=0 | B．a＜0，4a+b=0 |
| C．a＞0，2a+b=0 | D．a＜0，2a+b=0 |
已知定义在R上的函数f(x)，其导函数f′(x)的图象如图所示，则下列叙述正确的是( )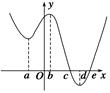
| A．f(b)>f(c)>f(d) |
| B．f(b)>f(a)>f(e) |
| C．f(c)>f(b)>f(a) |
| D．f(c)>f(e)>f(d) |
已知函数
，则不等式x+（x+1）f（x+1）≤1的解集是（ ）
A． | B．{x|x≤1} |
C． | D． |