题目内容
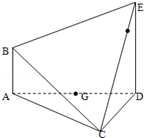
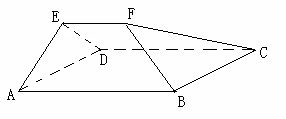
如图,正方形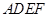 与梯形
与梯形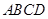 所在的平面互相垂直,
所在的平面互相垂直,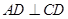 ,
, ∥
∥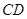 ,
,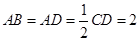 ,点
,点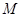 在线段
在线段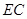 上.
上.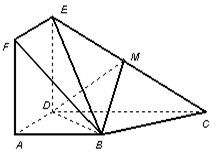
(I)当点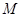 为
为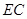 中点时,求证:
中点时,求证: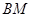 ∥平面
∥平面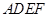 ;
;
(II)当平面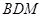 与平面
与平面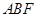 所成锐二面角的余弦值为
所成锐二面角的余弦值为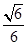 时,求三棱锥
时,求三棱锥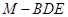 的体积.
的体积.
(I)建立空间直角坐标系,证明 ,进而得证;(II)
,进而得证;(II)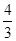
解析试题分析:
(I )以直线DA,BC,DE分别为x轴,y轴,z轴建立空间直角坐标系,
则 ,所以
,所以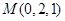 ,
,
所以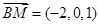 , 2分
, 2分
又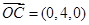 是平面
是平面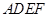 的一个法向量,
的一个法向量,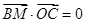 ,所以
,所以 ,
,
所以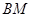 ∥平面
∥平面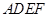 . 4分
. 4分
(II)设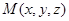 ,则
,则 ,又
,又 ,
,
则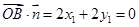 ,
,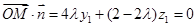 ,
,
取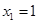 得
得  , 即
, 即  ,
,
又由题设, 是平面
是平面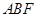 的一个法向量, 8分
的一个法向量, 8分
∴ 10分
10分
即点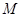 为
为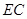 中点,此时,
中点,此时, ,
,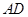 为三棱锥
为三棱锥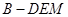 的高,
的高,
∴ 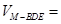
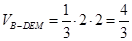 . 12分
. 12分
考点:本小题主要考查线面平行,二面角,三棱锥的体积计算.
点评:解决立体几何问题,可以用相关的定理证明,也可以用空间向量证明,利用空间向量也要依据相应的判定定理和性质定理,并且要注意各个角的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
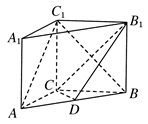
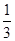 BB1,C1F=
BB1,C1F=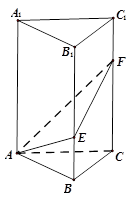
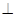 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
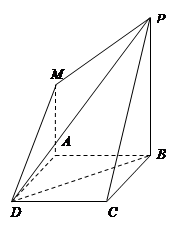
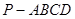 中,
中, 底面
底面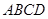 ,
,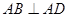 ,
,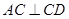 ,
,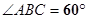 ,
,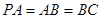 ,
,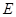 是
是 的中点.
的中点.
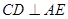 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.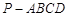 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,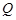 是棱
是棱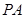 上的动点.
上的动点.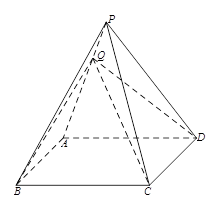
 是
是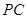 //平面
//平面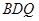 ;
;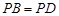 ,求证:
,求证: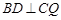 ;
;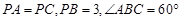 ,求四棱锥
,求四棱锥