题目内容
点P是曲线y=x2-lnx上任意一点,则点P到直线y=x+2的距离的最小值是 .
【答案】分析:求出平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标,再利用点到直线的距离公式可得结论.
解答:解:设P(x,y),则y′=2x- (x>0)
(x>0)
令2x- =1,则(x-1)(2x+1)=0,
=1,则(x-1)(2x+1)=0,
∵x>0,∴x=1
∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1)
由点到直线的距离公式可得d= =
=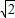
故答案为:
点评:本题考查导数知识的运用,考查点到直线的距离公式,考查学生的计算能力,属于基础题.
解答:解:设P(x,y),则y′=2x-
 (x>0)
(x>0)令2x-
 =1,则(x-1)(2x+1)=0,
=1,则(x-1)(2x+1)=0,∵x>0,∴x=1
∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1)
由点到直线的距离公式可得d=
 =
=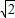
故答案为:

点评:本题考查导数知识的运用,考查点到直线的距离公式,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
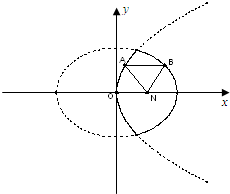 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆