题目内容
【题目】若函数![]()
![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)设![]() 的两个极值点为
的两个极值点为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1) 求函数的导数,利用![]() 在
在![]() 有两个不同根,转化为函数
有两个不同根,转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,从而
上有两个不同交点,从而![]() 极大值
极大值![]() ,利用数形结合所以要想函数
,利用数形结合所以要想函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() ,可得
,可得![]() 的取值范围;
的取值范围;
(2)由(1)利用![]() 在
在![]() 上单调性质可得试比较
上单调性质可得试比较![]() 与
与![]() 的大小;
的大小;
(3)证明![]() 等价于证明
等价于证明![]() ,
,
令![]() ,则
,则![]() ,等价于
,等价于![]() 的最小值大于0即可.
的最小值大于0即可.
解:(1)由已知![]() 得函数定义域为
得函数定义域为![]() ,
,
则![]() 在
在![]() 有两个不同的根,
有两个不同的根,
又![]() ,
,
即方程![]() 在
在![]() 上有两个不同的根,
上有两个不同的根,
转化为函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同的交点,
上有两个不同的交点,
又![]() ,
,
即![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
从而![]() ,
,
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时,![]() ,在
,在![]() 时,
时,![]() ,
,
所以要想函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同的交点,
上有两个不同的交点,
只需![]() ,
,
即![]() ;
;
(2)由(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() ,
,
即![]() ,
,
即![]() ,
,
所以![]() ;
;
(3)设![]() 的两个极值点为
的两个极值点为![]() ,由(1)可知
,由(1)可知![]() 分别是方程
分别是方程![]() 的两个根,
的两个根,
即![]() ,
,
设![]() ,作差得,
,作差得,
![]() ,即
,即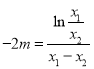 ,
,
要证明不等式![]() ,即等价于证明
,即等价于证明
![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
则函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
即不等式![]() 成立,
成立,
故所证不等式![]() 成立.
成立.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城.其中著名的景点有黄鹤楼、户部巷、东湖风景区等等.
(1)为了解“五·一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在22岁到52岁的游客中随机抽取了1000人,制成了如图的频率分布直方图:
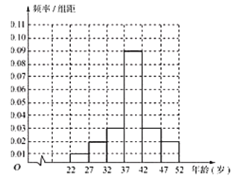
现从年龄在![]() 内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在
内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() ;
;
(2)为了给游客提供更舒适的旅游体验,该旅游景点游船中心计划在2020年劳动节当日投入至少1艘至多3艘![]() 型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量
型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量![]() (单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
(单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
劳动节当日客流量 |
|
|
|
频数(年) | 2 | 4 | 4 |
以这10年的数据资料记录的3个区间客流量的频率作为每年客流量在该区间段发生的概率,且每年劳动节当日客流量相互独立.
该游船中心希望投入的![]() 型游船尽可能被充分利用,但每年劳动节当日
型游船尽可能被充分利用,但每年劳动节当日![]() 型游船最多使用量(单位:艘)要受当日客流量
型游船最多使用量(单位:艘)要受当日客流量![]() (单位:万人)的影响,其关联关系如下表:
(单位:万人)的影响,其关联关系如下表:
劳动节当日客流量 |
|
| |
| 1 | 2 | 3 |
若某艘![]() 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘
型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘![]() 型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记
型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记![]() (单位:万元)表示该游船中心在劳动节当日获得的总利润,
(单位:万元)表示该游船中心在劳动节当日获得的总利润,![]() 的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘
的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘![]() 型游船才能使其当日获得的总利润最大?
型游船才能使其当日获得的总利润最大?