题目内容
(8分)已知函数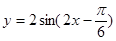 .
.
(1)写出它的振幅、周期、频率和初相;
(2)求这个函数的单调递减区间;
(3)求出使这个函数取得最大值时,自变量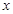 的取值集合,并写出最大值。
的取值集合,并写出最大值。
【答案】
(1)振幅2,周期 ,频率
,频率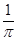 ,初相
,初相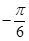 (2)
(2)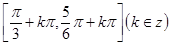
(3)当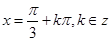 ,函数有最大值
,函数有最大值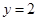
【解析】
试题分析:(1)振幅2,周期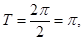 ,频率
,频率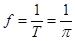 ,初相
,初相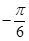 (2)令
(2)令 整理得
整理得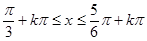 (3)函数最大值为2,此时需满足
(3)函数最大值为2,此时需满足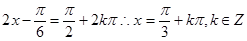
考点:三角函数性质
点评:三角函数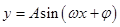 最值由振幅A决定,周期由
最值由振幅A决定,周期由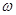 决定,平移由
决定,平移由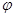 决定,求增区间令
决定,求增区间令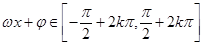 ,求减区间令
,求减区间令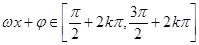 ,在高考题中已知条件常给出一个较复杂的三角函数式,需要考生利用诱导公式,和差角的正余弦公式,二倍角公式等将其化简为
,在高考题中已知条件常给出一个较复杂的三角函数式,需要考生利用诱导公式,和差角的正余弦公式,二倍角公式等将其化简为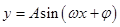 的形式
的形式

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 .
. 时,判断函数
时,判断函数 的奇偶性;
的奇偶性; 的解集为A,且
的解集为A,且 ,求实数
,求实数 的取值范围.
的取值范围.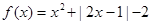 。
。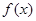 的图象;
的图象;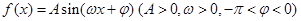 .
.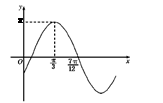
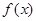 的部分图象如图所示,求
的部分图象如图所示,求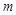
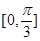 上是单调递增函数,求
上是单调递增函数,求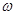 的最大值.
的最大值. 是奇函数,并且函数
是奇函数,并且函数 的图像经过点
的图像经过点 ,
,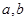 的值;
的值; 时的值域.
时的值域.