题目内容
设关于x的方程是x2-(tanθ+i)x-(2+i)=0,(1)若方程有实根,求锐角θ和实数根;
(2)求证:对任意θ≠kπ+![]() (k∈Z)方程无纯虚数根.
(k∈Z)方程无纯虚数根.
(1)解:设方程的实根为a,则a2-(tanθ+i)a-(2+i)=0,
即a2-tanθ·a-2-(a+1)i=0.
∵a·tanθ∈R,∴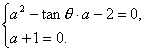
∴a=-1且tanθ=1.
又0<θ<![]() ,∴θ=
,∴θ=![]() ,a=-1.
,a=-1.
(2)证明:假设方程有纯虚数根bi(b∈R,b≠0),则
(bi)2-(tanθ+i)·bi-(2+i)=0.
∴-b2+b-2=0, ①
且-tanθ·b-1=0. ②
由②得b=-cotθ,代入①得cot2θ+cotθ+2=0,此方程Δ=1-8<0,∴cotθ为虚数,与cotθ∈R矛盾,假设不成立.∴原方程对于任意实数θ不可能有纯虚数根.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目


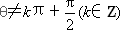 方程无纯虚数根.
方程无纯虚数根.