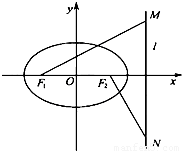
题目内容
设椭圆C:
+y2=1(λ>0)的两焦点是F1,F2,且椭圆上存在点P,使
•
=0
(1)求实数λ的取值范围;
(2)若直线l:x-y+2=0与椭圆C存在一公共点M,使得|MF1|+|MF2|取得最小值,求此最小值及此时椭圆的方程.
(3)在条件(2)下的椭圆方程,是否存在斜率为k(k≠0)的直线?,与椭圆交于不同的两点A、B,满足
=
,且使得过点Q,N(0,-1)两点的直线NQ满足
•
=0?若存在,求出k的取值范围;若不存在,说明理由.
| x2 |
| λ+1 |
| PF1 |
| PF2 |
(1)求实数λ的取值范围;
(2)若直线l:x-y+2=0与椭圆C存在一公共点M,使得|MF1|+|MF2|取得最小值,求此最小值及此时椭圆的方程.
(3)在条件(2)下的椭圆方程,是否存在斜率为k(k≠0)的直线?,与椭圆交于不同的两点A、B,满足
| AQ |
| QB |
| NQ |
| AB |
解(1)由椭圆定义可得:|PF1|+|PF2|=2
由
1•
=0可得|PF1|2+|PF2|2=4λ
而|PF1|2+|PF2|2≥
∴4λ≥2(λ+1)解得λ≥1(3分).
(2)由x-y+2=0,
+y2=1,得(λ+2)x2+4(λ+1)x+3(λ+1)=0
△=16(λ+1)2-12(λ+2)(λ+1)=4(λ+1)(λ-2)≥0•
解得λ≥2或λ≤-1(舍去)∴λ≥2此时|MF1|+|MF2|=2
≥2
当仅当λ=2时,|MF1|+|MF2|取得最小值2
,此时椭圆方程为
+y2=1(8分)
(3)由
=
知点Q是AB的中点.设两点A(x1,y1),B(x2,y2),中点Q(x,y),则
+y12=1
+y22=1两式相减得
+(y1-y2)(y1+y2)=0
∴
=-
∴AB中点Q(x,y)的轨迹为直线y=-
x①
且在椭圆内的部分.又由
•
=0可知,NQ⊥AB,
所以直线NQ的斜率为-
,方程为y=-
x-1②
联立①、②可求得点Q的坐标为(-
,
)
∵点Q必在椭圆内,
+(
),1,解得k2<1
又∵k≠0,∴k∈(-1,0)∪(0,1)(12分)
| λ+1 |
| PF |
| PF2 |
而|PF1|2+|PF2|2≥
| (|PF1|+|PF2|)2 |
| 2 |
(2)由x-y+2=0,
| x2 |
| λ+1 |
△=16(λ+1)2-12(λ+2)(λ+1)=4(λ+1)(λ-2)≥0•
解得λ≥2或λ≤-1(舍去)∴λ≥2此时|MF1|+|MF2|=2
| λ+1 |
| 3 |
当仅当λ=2时,|MF1|+|MF2|取得最小值2
| 3 |
| x2 |
| 3 |
(3)由
| AQ |
| QB |
| x12 |
| 3 |
| x22 |
| 3 |
| (x 1+x2)(x1-x2) |
| 3 |
∴
| y2-y1 |
| x2-x1 |
| x2+x1 |
| 3(y2+y1) |
| 1 |
| 3k |
且在椭圆内的部分.又由
| NQ |
| AB |
所以直线NQ的斜率为-
| 1 |
| k |
| 1 |
| k |
联立①、②可求得点Q的坐标为(-
| 3k |
| 2 |
| 1 |
| 2 |
∵点Q必在椭圆内,
(-
| ||
| 3 |
| 1 |
| 2 |
又∵k≠0,∴k∈(-1,0)∪(0,1)(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•闸北区二模)设椭圆C:x2+2y2=2b2(常数b>0)的左右焦点分别为F1,F2,M,N是直线l:x=2b上的两个动点,
(2012•闸北区二模)设椭圆C:x2+2y2=2b2(常数b>0)的左右焦点分别为F1,F2,M,N是直线l:x=2b上的两个动点,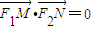 .
.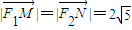 ,求b的值;
,求b的值;
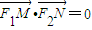 .
.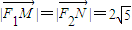 ,求b的值;
,求b的值;