题目内容
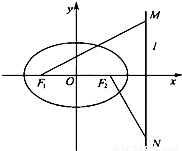
设椭圆C:x2+2y2=2b2(常数b>0)的左右焦点分别为F1,F2,M,N是直线l:x=2b上的两个动点,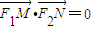 .
.(1)若
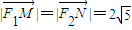 ,求b的值;
,求b的值;(2)求|MN|的最小值.
【答案】分析:(1)设M(2b,y1),N(2b,y2),根据椭圆方程得到椭圆左、右焦点的坐标,从而得到向量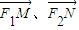 的坐标,结合向量数量积的坐标公式和向量模的公式建立关于b、y1、y2的方程组,消去y1、y2,可得正数b的值.
的坐标,结合向量数量积的坐标公式和向量模的公式建立关于b、y1、y2的方程组,消去y1、y2,可得正数b的值.
(2)由(1)设的坐标,得|MN|=|y1-y2|,将其平方再用基本不等式,即可得到当且仅当y1、y2互为相反数且其中一个为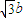 时,|MN|2的最小值为12b2,由此得到|MN|的最小值.
时,|MN|2的最小值为12b2,由此得到|MN|的最小值.
解答:解:设M(2b,y1),N(2b,y2)…(1分)
∵椭圆方程为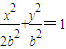 ,∴椭圆的左右焦点分别为F1(-b,0),F2(b,0),
,∴椭圆的左右焦点分别为F1(-b,0),F2(b,0),
由此可得: ,
,
∵ ,∴3b•b+y1y2=0,得
,∴3b•b+y1y2=0,得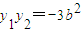 ①…(3分)
①…(3分)
(1)由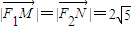 ,得
,得
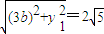 …②,
…②,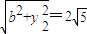 ③…(5分)
③…(5分)
由①、②、③三式,消去y1,y2,可得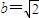 . …(8分)
. …(8分)
(2)∵M(2b,y1),N(2b,y2),
∴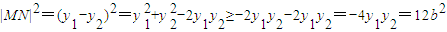 ,(12分)
,(12分)
当且仅当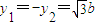 或
或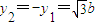 时,|MN|取最小值
时,|MN|取最小值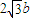 . …(14分)
. …(14分)
点评:本题以平面向量的坐标运算为载体,考查了椭圆的标准方程、简单几何性质和向量的数量积运算等知识,属于基础题.
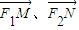 的坐标,结合向量数量积的坐标公式和向量模的公式建立关于b、y1、y2的方程组,消去y1、y2,可得正数b的值.
的坐标,结合向量数量积的坐标公式和向量模的公式建立关于b、y1、y2的方程组,消去y1、y2,可得正数b的值.(2)由(1)设的坐标,得|MN|=|y1-y2|,将其平方再用基本不等式,即可得到当且仅当y1、y2互为相反数且其中一个为
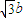 时,|MN|2的最小值为12b2,由此得到|MN|的最小值.
时,|MN|2的最小值为12b2,由此得到|MN|的最小值.解答:解:设M(2b,y1),N(2b,y2)…(1分)
∵椭圆方程为
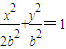 ,∴椭圆的左右焦点分别为F1(-b,0),F2(b,0),
,∴椭圆的左右焦点分别为F1(-b,0),F2(b,0),由此可得:
 ,
,∵
 ,∴3b•b+y1y2=0,得
,∴3b•b+y1y2=0,得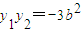 ①…(3分)
①…(3分)(1)由
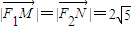 ,得
,得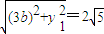 …②,
…②,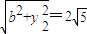 ③…(5分)
③…(5分)由①、②、③三式,消去y1,y2,可得
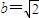 . …(8分)
. …(8分)(2)∵M(2b,y1),N(2b,y2),
∴
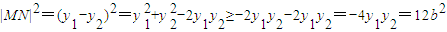 ,(12分)
,(12分)当且仅当
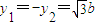 或
或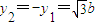 时,|MN|取最小值
时,|MN|取最小值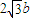 . …(14分)
. …(14分)点评:本题以平面向量的坐标运算为载体,考查了椭圆的标准方程、简单几何性质和向量的数量积运算等知识,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 (2012•江苏二模)选做题
(2012•江苏二模)选做题 .
.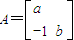 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值. =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值.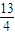 ,求x+y+z的最大值.
,求x+y+z的最大值.