题目内容
已知A(-4,0),B(2,0)以AB为直径的圆与y轴的负半轴交于C,求过C点的圆的切线方程.
分析:求出以AB为直径的圆的方程,求出圆与y轴的负半轴交于C的坐标,然后求出C与圆心连线的斜率,求出切线的斜率,即可求出切线方程.
解答:解:已知A(-4,0),B(2,0)以AB为直径的圆的方程为:(x+4)(x-2)+y2=0
以AB为直径的圆与y轴的负半轴交于C(0,-2
),圆心与C连线的斜率为:-2
所以切线的斜率为:
=
所以切线方程为:y+2
=
x-0)即:
x-4y-8
=0
过C点的圆的切线方程:
x-4y-8
=0
以AB为直径的圆与y轴的负半轴交于C(0,-2
| 2 |
| 2 |
所以切线的斜率为:
| 1 | ||
2
|
| ||
| 4 |
所以切线方程为:y+2
| 2 |
| ||
| 4 |
| 2 |
| 2 |
过C点的圆的切线方程:
| 2 |
| 2 |
点评:本题是基础题,考查圆的直径式方程,圆的切线方程的求法,注意抓好转化思想的训练,在解题中经常使用,是常考题.

练习册系列答案
相关题目
 如图所示,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是
如图所示,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是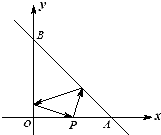 如图,已知A(4,0)、B(4,0),从点P(1,0)射出的光线经直线AB反向后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
如图,已知A(4,0)、B(4,0),从点P(1,0)射出的光线经直线AB反向后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )