题目内容
（本小题满分１４分）
设函数
.
(1)求函数
的单调区间;
(2)当
时,不等式恒成立,求实数
的取值范围;
(3)关于
的方程
在
上恰有两个相异实根,求
的取值范围.
（本小题满分１４分）
解:(1)函数定义域为
.……1分
.……2分
由
得
或
; 由
得
或
.
因此递增区间是
; 递减区间是
.……4分
(2)由(1)知,
在
上递减,在
上递增. ……5分
又
且
,
所以
时,
. ……8分
故
时,不等式恒成立. ……9分
(3)方程
即
.
记
,则
.……10分
由
得
或
; 由
得
.
所以
在
上递减,在
上递增. ……11分
为使
在
上恰好有两个相异的实根,只须
在
和
上各有一个实根,于是有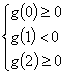
,解得
.……13分
故实数
的取值范围是.……14分
练习册系列答案
相关题目
（m为常数，m>0且
）
是首项为4，公差为2的等差数列. 
，且数列{bn}的前n项和Sn，当
时，求Sn；
和定直线
，
是定直线
,动点
满足
，
（其中
为坐标原点）.
的方程;
的直线
与
两点
的值;
,当三角形
的面积
时,求
的取值范围.
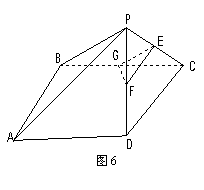如图5，在直角梯形ABCP中，AP//BC，AP
AB，AB=BC=
，D是AP的中点，E，F，G分别为PC、PD、CB的中点，将
沿CD折起，使得
平面ABCD, 如图6.
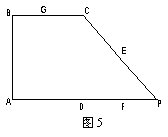（Ⅰ）求证：AP//平面EFG；
的大小；
的体积.