题目内容
20.记定点M ($\frac{5}{2}$,3)与抛物线y2=2x上的点P之间的距离为d1,P到抛物线的准线l距离为d2,则d1+d2的最小值为( )| A. | $\sqrt{13}$ | B. | 2$\sqrt{13}$ | C. | 13 | D. | 3 |
分析 如图所示,由抛物线y2=2x,可得焦点F($\frac{1}{2}$,0).过点P作PE⊥准线,垂足为E点.利用抛物线的定义可得:PE=PF.于是d1+d2=|PF|+|PM|=|PF|+|PM|≥|FM|.再利用两点间的距离公式即可得出.
解答 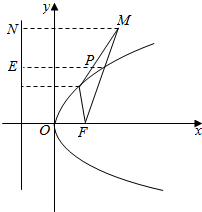 解:如图所示,
解:如图所示,
由抛物线y2=2x,可得焦点F($\frac{1}{2}$,0).
过点P作PE⊥准线,垂足为E点.
则PE=PF.
∴d1+d2=|PF|+|PM|=|PF|+|PM|≥|FM|.
∴d1+d2的最小值=|FM|=$\sqrt{(\frac{5}{2}-\frac{1}{2})^{2}+{3}^{2}}$=$\sqrt{13}$.
故选:A.
点评 本题考查了抛物线的定义、两点间的距离公式、三角形的两边之间的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列语句不是命题的是( )
| A. | 祁阳一中是一所一流名校 | |
| B. | 如果这道题做不到,那么这次考试成绩不理想 | |
| C. | ?x∈R,使得lnx0<0 | |
| D. | 画一个椭圆 |
9.设x∈R,则命题q:x>-1是命题p:x>0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |




 已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是45°.
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是45°.