题目内容
例1、已知函数f(x)=
的定义域为A,函数y=f[f(x)]的定义域为B,则( )
| 1+x |
| 1-x |
| A、A∪B=B | B、A不属于B |
| C、A=B | D、A∩B=B |
分析:根据题意,由分式函数的定义域可得集合A,由解析式的求法可得函数y=f[f(x)]的解析式,进而可得集合B,分析A、B可得答案.
解答:解:根据题意,已知函数f(x)=
的定义域为A,则A={x|x≠1},
y=f[f(x)]=f(
)=f(-1+
)=-
,
令-1+
≠1且x≠1,故B={x|x≠1}∩{x|x≠0},
即B?A,则必有A∩B=B;
故选D.
| 1+x |
| 1-x |
y=f[f(x)]=f(
| 1+x |
| 1-x |
| 2 |
| 1-x |
| 1 |
| x |
令-1+
| 2 |
| 1-x |
即B?A,则必有A∩B=B;
故选D.
点评:本题重点考查函数定义域的求法,注意复合函数的定义域的求法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
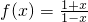 的定义域为A,函数y=f[f(x)]的定义域为B,则
的定义域为A,函数y=f[f(x)]的定义域为B,则 的定义域为A,函数y=f[f(x)]的定义域为B,则( )
的定义域为A,函数y=f[f(x)]的定义域为B,则( ) 的定义域为A,函数y=f[f(x)]的定义域为B,则( )
的定义域为A,函数y=f[f(x)]的定义域为B,则( )