题目内容
已知向量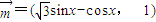 ,
,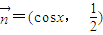 ,若
,若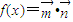 .
.(1) 求函数f(x)的最小正周期;
(2) 已知△ABC的三内角A、B、C的对边分别为a、b、c,且
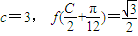 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.
【答案】分析:(1)利用向量的数量积公式表示出f(x);利用三角函数的二倍角公式及公式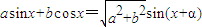
利用三角函数的周期公式求出周期.
(2)先求出角C,利用正弦定理将三角函数的关系转化为边的关系在,再利用余弦定理求出边.
解答:解:(1)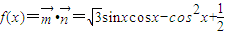
=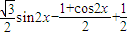
=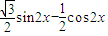
= (4分)
(4分)
∴f(x)的最小正周期为π.(6分)
(2)∵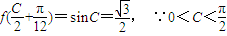 ,∴
,∴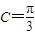 (8分)
(8分)
∵2sinA=sinB.由正弦定理得b=2a,①(9分)
∵c=3,由余弦定理,得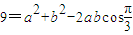 ,②(10分)
,②(10分)
解①②组成的方程组,得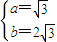 . (12分)
. (12分)
点评:本题考查向量的数量积公式、考查三角函数的二倍角公式、考查三角函数的和差角公式、考查三角形中的正弦定理余弦定理.
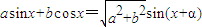
利用三角函数的周期公式求出周期.
(2)先求出角C,利用正弦定理将三角函数的关系转化为边的关系在,再利用余弦定理求出边.
解答:解:(1)
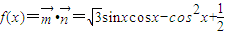
=
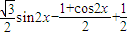
=
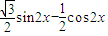
=
 (4分)
(4分)∴f(x)的最小正周期为π.(6分)
(2)∵
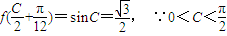 ,∴
,∴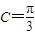 (8分)
(8分)∵2sinA=sinB.由正弦定理得b=2a,①(9分)
∵c=3,由余弦定理,得
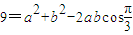 ,②(10分)
,②(10分)解①②组成的方程组,得
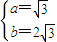 . (12分)
. (12分)点评:本题考查向量的数量积公式、考查三角函数的二倍角公式、考查三角函数的和差角公式、考查三角形中的正弦定理余弦定理.

练习册系列答案
相关题目
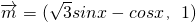 ,
,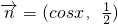 ,若
,若 .
.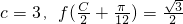 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.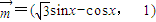 ,
,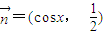 ,若
,若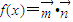 .
.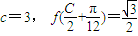 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.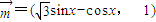 ,
,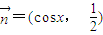 ,若
,若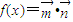 .
.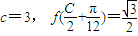 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.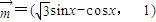 ,
,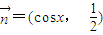 ,若
,若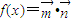 .
.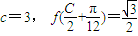 (C为锐角),2sinA=sinB,求C、a、b的值.
(C为锐角),2sinA=sinB,求C、a、b的值.