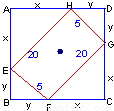
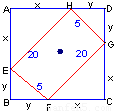
题目内容
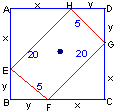 把一个长、宽、高分别为25cm、20cm、5cm的长方体木盒从一个正方形窗口穿过,那么正方形窗口的边长至少应为
把一个长、宽、高分别为25cm、20cm、5cm的长方体木盒从一个正方形窗口穿过,那么正方形窗口的边长至少应为分析:由于长方体各个面中宽和高所在的面的边长最小,所以应由这个面对称地穿过窗口才能使正方形窗口边长尽量地小,若设AE=x,BE=y,(x>0,y>0),则有AE=AH=CF=CG=x,BE=BF=DG=DH=y;由题意列方程组
,解得x,y;从而得正方形窗口的边长最小为AB=x+y.
|
解答:解:由于长方体各个面中宽和高所在的面的边长最小,所以应由这个面对称地穿过窗口才能使正方形窗口边长尽量地小.如图所示,设AE=x,BE=y,(其中x>0,y>0),则有AE=AH=CF=CG=x,BE=BF=DG=DH=y;
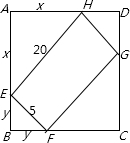
由题意,得
,解得
;∴AB=x+y=10
+
=
;
所以,正方形窗口的边长至少应为
cm.

由题意,得
|
|
| 2 |
5
| ||
| 2 |
25
| ||
| 2 |
所以,正方形窗口的边长至少应为
25
| ||
| 2 |
点评:本题实际上是考查求正方形窗口边长的最小值问题,考查了运用所学知识、思想和方法来解决实际问题的数学建模能力,是基础题.

练习册系列答案
相关题目