题目内容
下列四个命题:①在区间[0,1]内任取两个实数x,y,则事件“x2+y2>1恒成立”的概率是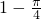 ; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,
; ②从200个元素中抽取20个样本,若采用系统抽样的方法则应分为10组,每组抽取2个; ③函数f(x)关于(3,0)点对称,满足f(6+x)=f(6-x),且当x∈[0,3]时函数为增函数,则f(x)在[6,9]上为减函数; ④满足A=30°,BC=1,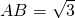 的△ABC有两解.其中正确命题的个数为
的△ABC有两解.其中正确命题的个数为
- A.1
- B.2
- C.3
- D.4
C
分析:①本题是一个几何概型,试验发生包含的事件对应的集合是Ω={(x,y)|-1<x<1,-1<y<1},满足条件的事件对应的集合是A={(x,y)|-1<x<1,-1<y<1,x2+y2>1},做出两个集合对应的图形的面积,根据几何概型概率公式得到结果.②根据系统抽样的定义,可知此命题是假命题;③根据函数f(x)关于(3,0)点对称,且当x∈[0,3]时函数为增函数,以及中心对称图象的单调性的性质可知函数f(x)在区间(3,6)是增函数,由f(6+x)=f(6-x),可知函数f(x)的图象关于直线x=6对称,根据轴对称图形的单调性的特征可知结论;④利用余弦定理解方程 ,即可求得结果.
,即可求得结果.
解答:①由题意知本题是一个几何概型,
试验发生包含的事件对应的集合是Ω={(x,y)|0≤x≤1,0≤y≤1},
它的面积是1×1=1,
满足条件的事件对应的集合是A={(x,y)|0≤x≤1,0≤y≤1,x2+y2>1}
集合A对应的图形的面积是边长为1的正方形内部,且圆的外部,面积是1-
∴根据几何概型的概率公式得到P=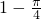 ,故正确;
,故正确;
②从200个元素中抽取20个样本,间隔为10,而不是分成10组,故错;
③∵函数f(x)关于(3,0)点对称,且当x∈[0,3]时函数为增函数,
∴函数f(x)在区间(3,6)是增函数,
∵f(6+x)=f(6-x),
∴函数f(x)的图象关于直线x=6对称,
故f(x)在[6,9]上为减函数;该命题正确;
④由余弦定理可知cosA= ,
,
整理得AC2-3AC+2=0,求得AC=1或2,因此△ABC有两解,故正确,
故选C.
点评:此种题型往往比较综合考查多个知识点的概念,处理的关键是熟练掌握各个知识点的概念、定义.同时考查了学生的思维转换和运算能力,属中档题.
分析:①本题是一个几何概型,试验发生包含的事件对应的集合是Ω={(x,y)|-1<x<1,-1<y<1},满足条件的事件对应的集合是A={(x,y)|-1<x<1,-1<y<1,x2+y2>1},做出两个集合对应的图形的面积,根据几何概型概率公式得到结果.②根据系统抽样的定义,可知此命题是假命题;③根据函数f(x)关于(3,0)点对称,且当x∈[0,3]时函数为增函数,以及中心对称图象的单调性的性质可知函数f(x)在区间(3,6)是增函数,由f(6+x)=f(6-x),可知函数f(x)的图象关于直线x=6对称,根据轴对称图形的单调性的特征可知结论;④利用余弦定理解方程
 ,即可求得结果.
,即可求得结果.解答:①由题意知本题是一个几何概型,
试验发生包含的事件对应的集合是Ω={(x,y)|0≤x≤1,0≤y≤1},
它的面积是1×1=1,
满足条件的事件对应的集合是A={(x,y)|0≤x≤1,0≤y≤1,x2+y2>1}
集合A对应的图形的面积是边长为1的正方形内部,且圆的外部,面积是1-

∴根据几何概型的概率公式得到P=
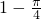 ,故正确;
,故正确;②从200个元素中抽取20个样本,间隔为10,而不是分成10组,故错;
③∵函数f(x)关于(3,0)点对称,且当x∈[0,3]时函数为增函数,
∴函数f(x)在区间(3,6)是增函数,
∵f(6+x)=f(6-x),
∴函数f(x)的图象关于直线x=6对称,
故f(x)在[6,9]上为减函数;该命题正确;
④由余弦定理可知cosA=
 ,
,整理得AC2-3AC+2=0,求得AC=1或2,因此△ABC有两解,故正确,
故选C.
点评:此种题型往往比较综合考查多个知识点的概念,处理的关键是熟练掌握各个知识点的概念、定义.同时考查了学生的思维转换和运算能力,属中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目