题目内容
有一个正四面体的棱长为3,现用一张圆形的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 .
分析:本题转化为四面体的侧面展开问题.在解答时,首先要将四面体的三个侧面沿底面展开,观察展开的图形易知包装纸的对角线处在什么位置时,包装纸面积最小,进而获得问题的解答.
解答:解:由题意,将正四面体沿底面将侧面都展开,如图所示:
设底面正三角形的中心为O,不难得到当以SO为圆的半径时,
所需包装纸的半径最小,
此时SO=
+
×
=2
,
故答案为:2
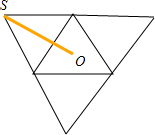
设底面正三角形的中心为O,不难得到当以SO为圆的半径时,
所需包装纸的半径最小,
此时SO=
3
| ||
| 2 |
3
| ||
| 2 |
| 1 |
| 3 |
| 3 |
故答案为:2
| 3 |

点评:本题考查的是棱锥的结构特征、四面体的侧面展开问题.在解答的过程当中充分体现了侧面展开的处理问题方法、图形的观察和分析能力以及问题转化的思想.值得同学们体会反思.

练习册系列答案
相关题目
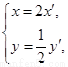 ,现用一张圆形的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 .
,现用一张圆形的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 .