题目内容
设数列 为等差数列,其前n项和为
为等差数列,其前n项和为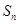 ,已知
,已知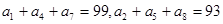 ,若对任意
,若对任意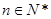 都有
都有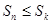 成立,则k的值为( )
成立,则k的值为( )
| A.22 | B.21 | C.20 | D.19 |
C
解析试题分析:因为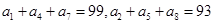 ,
,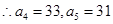 ,所以数列
,所以数列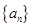 是以
是以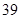 为首项,
为首项,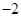 为公差的等差数列,对任意
为公差的等差数列,对任意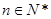 都有
都有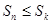 成立,则为数列
成立,则为数列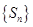 的最大项,而在数列
的最大项,而在数列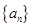 中,
中,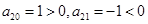 ,故
,故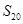 为数列
为数列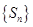 的最大项.
的最大项.
考点:等差数列的运算性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等比数列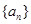 公比为
公比为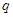 ,其前
,其前 项和为
项和为 ,若
,若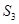 、
、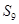 、
、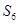 成等差数列,则
成等差数列,则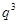 等于( )
等于( )
A.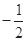 | B.1 | C.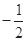 或1 或1 | D.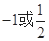 |
若数列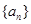 的前n项和为
的前n项和为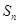 ,则下列命题:
,则下列命题:
(1)若数列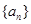 是递增数列,则数列
是递增数列,则数列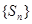 也是递增数列;
也是递增数列;
(2)数列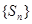 是递增数列的充要条件是数列
是递增数列的充要条件是数列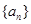 的各项均为正数;
的各项均为正数;
(3)若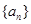 是等差数列(公差
是等差数列(公差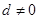 ),则
),则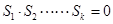 的充要条件是
的充要条件是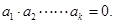
(4)若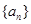 是等比数列,则
是等比数列,则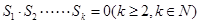 的充要条件是
的充要条件是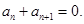
其中,正确命题的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
在等差数列 中,2a4+a7=3,则数列
中,2a4+a7=3,则数列 的前9项和等于( )
的前9项和等于( )
| A.9 | B.6 | C.3 | D.12 |
等差数列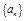 中的
中的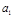 、
、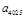 是函数
是函数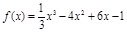 的极值点,则
的极值点,则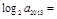 ( )
( )
A.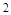 | B.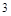 | C.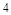 | D.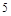 |
等差数列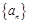 的前
的前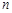 项和为
项和为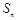 ,若
,若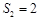 ,
,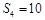 ,则
,则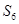 等于( )
等于( )
| A.12 | B.18 | C.24 | D.42 |
如果等差数列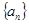 中,
中,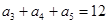 ,那么
,那么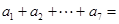 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
设Sn是等差数列{an}的前n项和,若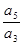 =
=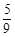 ,则
,则 = ( ).
= ( ).
| A.1 | B.-1 | C.2 | D.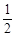 |
下面是关于公差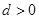 的等差数列
的等差数列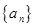 的四个命题
的四个命题
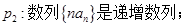
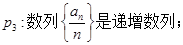

其中的真命题为( )
A.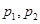 | B.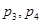 | C.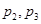 | D.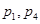 |